题目内容
2.设α∈(0,$\frac{π}{2}$),若sinα=$\frac{3}{5}$,则$\sqrt{2}$cos(α+$\frac{π}{4}$)等于( )| A. | $\frac{7}{5}$ | B. | $\frac{1}{5}$ | C. | -$\frac{7}{5}$ | D. | -$\frac{1}{5}$ |
分析 利用同角三角函数基本关系式求出余弦函数值,然后利用两角和的余弦函数化简求解即可.
解答 解:α∈(0,$\frac{π}{2}$),sinα=$\frac{3}{5}$,可得cosα=$\frac{4}{5}$,
$\sqrt{2}$cos(α+$\frac{π}{4}$)=$\sqrt{2}$cosαcos$\frac{π}{4}$-$\sqrt{2}$sinαsin$\frac{π}{4}$=$\frac{4}{5}-$$\frac{3}{5}$=$\frac{1}{5}$.
故选:B.
点评 本题考查两角和与差的三角函数,同角三角函数基本关系式的应用,考查计算能力.

练习册系列答案
相关题目
 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AB,点M、N分别是线段A1C1,A1B的中点.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AB,点M、N分别是线段A1C1,A1B的中点.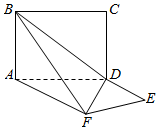 平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,则异面直线EF与BC所成角大小为30°.
平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,则异面直线EF与BC所成角大小为30°.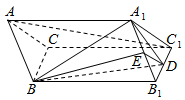 如图,在三棱柱ABC-A1B1C1中,A1B1=A1C1,点D,E分别是B1C1,A1B1的中点,AA1=AB=BD=1,∠A1AB=60°.
如图,在三棱柱ABC-A1B1C1中,A1B1=A1C1,点D,E分别是B1C1,A1B1的中点,AA1=AB=BD=1,∠A1AB=60°.