题目内容
已知等式|x-2|>1的解集与关于x的不等式x2-ax+b>0的解集相等.
(I)求实数a,b的值;
(Ⅱ)求函数f(x)=a
+b
的最大值.
(I)求实数a,b的值;
(Ⅱ)求函数f(x)=a
| x-3 |
| 4-x |
考点:绝对值不等式的解法,函数的最值及其几何意义
专题:不等式
分析:(Ⅰ)求出不等式|x-2|>1的解集,即得不等式x2-ax+b>0的解集,利用一元二次方程根与系数的关系求出 a和b的值,
(Ⅱ)根据柯西不等式即可求出最大值.
(Ⅱ)根据柯西不等式即可求出最大值.
解答:
解:(Ⅰ)由不等式|x-2|>1可得 x-2>1 或x-2<-1,解得x>3 或x<1,
故不等式|x-2|>1的解集为{x|x>3 或x<1 },
即不等式x2-ax+b>0的解集为{x|x>3 或x<1 }.
∴1,3为方程x2-ax+b=0的两根,
∴3+1=a,3×1=b,
∴a=4,b=3,
(Ⅱ)函数f(x)=4
+3
的定义域为[3,4],
由柯西不等式得f2(x)=(4
+3
)2≤(16+9)(x-3+4-x)=25,
又f(x)>0,
∴f(x)≤5,当且仅当4
=3
,即x=
时,f(x)=5,
∴函数f(x)=a
+b
的最大值为5.
故不等式|x-2|>1的解集为{x|x>3 或x<1 },
即不等式x2-ax+b>0的解集为{x|x>3 或x<1 }.
∴1,3为方程x2-ax+b=0的两根,
∴3+1=a,3×1=b,
∴a=4,b=3,
(Ⅱ)函数f(x)=4
| x-3 |
| 4-x |
由柯西不等式得f2(x)=(4
| x-3 |
| 4-x |
又f(x)>0,
∴f(x)≤5,当且仅当4
| x-3 |
| 4-x |
| 91 |
| 25 |
∴函数f(x)=a
| x-3 |
| 4-x |
点评:本题主要考查绝对值不等式的解法,一元二次方程根与系数的关系,以及柯西不等式,属于中档题.

练习册系列答案
相关题目
已知{an}是等比数列,(a6+a10)(a4+a8)=49,则a5+a9等于( )
| A、7 | B、±7 | C、14 | D、不确定 |
若0<a<1且b>1,则函数y=ax-b的图象不经过( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
过点P(-2,3)的抛物线的标准方程是( )
A、y2=-
| ||||
B、y2=
| ||||
C、y2=
| ||||
D、y2=-
|
下列有关命题的说法中,错误的是( )
| A、若“p或q”为假命题,则p,q均为假命题 | ||||
| B、“x=1”是“x≥1”的充分不必要条件 | ||||
C、“x=
| ||||
| D、若命题p:”?实数x0,使x02≥0”则命题?p:“对于?x∈R,都有x2<0” |
已知复数z=
,则复数z等于( )
| 1+2i |
| i |
| A、2-i | B、2+i |
| C、-2+i | D、-2-i |
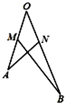 如图,M、N分别是线段OA、OB上的点,OM=MA=ON=1,NB=2,设
如图,M、N分别是线段OA、OB上的点,OM=MA=ON=1,NB=2,设