题目内容
如果椭圆
+
=1的弦被点（2，2）平分，则这条弦所在的直线方程是 ．
| x2 |
| 36 |
| y2 |
| 9 |
考点：直线与圆锥曲线的综合问题
专题：计算题,圆锥曲线的定义、性质与方程
分析：设这条弦的两端点为A（x1，y1），B（x2，y2），利用点差法，结合（2，2）为AB的中点，求出直线的斜率，即可求出弦所在的直线方程．
解答：
解：设这条弦的两端点为A（x1，y1），B（x2，y2），斜率为k，
∵（2，2）为AB的中点，
∴x1+x2=4，y1+y2=4，
∵x12+4y12=36，x22+4y22=36，
∴两式相减可得（x1+x2）（x1-x2）+4（y1+y2）（y1-y2）=0，
∴4（x1-x2）+16（y1-y2）=0，
∴k=
=-
，
∴弦所在的直线方程是y-2=-
（x-2），即x+4y-10=0．
故答案为：x+4y-10=0．
∵（2，2）为AB的中点，
∴x1+x2=4，y1+y2=4，
∵x12+4y12=36，x22+4y22=36，
∴两式相减可得（x1+x2）（x1-x2）+4（y1+y2）（y1-y2）=0，
∴4（x1-x2）+16（y1-y2）=0，
∴k=
| y1-y2 |
| x1-x2 |
| 1 |
| 4 |
∴弦所在的直线方程是y-2=-
| 1 |
| 4 |
故答案为：x+4y-10=0．
点评：本题考查直线与椭圆的位置关系，考查点差法的运用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
如图，函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|≤
下列函数中，以
为最小正周期的是（ ）
| π |
| 2 |
A、y=sin
| ||
| B、y=sinx | ||
| C、y=sin2x | ||
| D、y=sin4x |
如图给出的计算1+
+
+…+
的值的一个程序框图，则判断框内应填入的条件是（ ）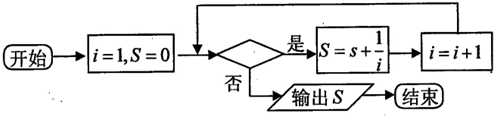
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2014 |
| A、i≤2014 |
| B、i＞2014 |
| C、i≤2013 |
| D、i＞2013 |