Question

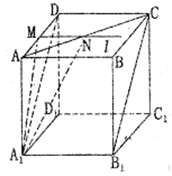在长方体ABCD-A₁B₁C₁D₁中，AB=

3

，AD=1，M是线段AD的中点．
（1）试过M点作出与平面A₁B₁CD平行的直线l，说明理由，并证明：l⊥平面AA₁D₁D；
（2）若（1）中的直线l交直线AC于点N，且二面角A-A₁N-M的余弦值为

15

5

，求AA₁的长．

Answer 1

考点：与二面角有关的立体几何综合题,直线与平面垂直的判定

专题：空间位置关系与距离

分析：（1）在平面ABCD内过M点作直线l∥CD，此时l满足l∥平面A₁B₁CD，由线面平行的判定定理可说明理由，进而结合长方体的几何特征和线面垂直的判定定理，可得l⊥平面AA₁D₁D；
（2）设AA₁=h，建立空间直角坐标系，分别求出平面AA₁N的一个法向量和平面A₁MN的一个法向量，代入向量夹角公式，结合二面角A-A₁N-M的余弦值为

15

5

，构造关于h的方程，解方程可得答案．

解答： 解：（1）在平面ABCD内过M点作直线l∥CD，
此时l满足l∥平面A₁B₁CD，理由如下：
∵l∥CD，l?平面A₁B₁CD，CD?平面A₁B₁CD，
∴l∥平面A₁B₁CD，
在长方体ABCD-A₁B₁C₁D₁中，
CD⊥AD，CD⊥DD₁，
又∵AD∩DD₁=D，AD，DD₁?平面AA₁D₁D，
∴CD⊥平面AA₁D₁D
又∵l∥CD，
∴l⊥平面AA₁D₁D；
（2）由（1）中，l∥CD，M是线段AD的中点．
可得N为直线AC的中点，
设AA₁=h，建立如图所示的空间直角坐标系，
则A₁（0，0，0），A（0，0，h），N（

3

2

，

1

2

，h），M（0，

1

2

，h），
∴

A1A

=（0，0，h），

A1N

=（

3

2

，

1

2

，h），

A1M

=（0，

1

2

，h），
设平面AA₁N的一个法向量为

m

=（x，y，z），
则

m • A1A =0 m • A1N =0

．即

hz=0 3 2 x+ 1 2 y+hz=0

，
令x=1，则

m

=（1，-

3

，0）

设平面A₁MN的一个法向量为

n

=（a，b，c），
则

n • A1M =0 m • A1N =0

，即

1 2 b+hc=0 3 2 a+ 1 2 b+hc=0

，
令c=1，则

n

=（0，-2h，1），
∵二面角A-A₁N-M的余弦值为

15

5

，
∴cos＜

m

，

n

＞=

2 3 h

2 1+4h2

=

15

5

，
解得h=1．
即求AA₁=1

点评：本题考查的知识点是与二面角有关的立体几何，直线与平面平行的判断，建立空间坐标系，将二面角问题转化为向量夹角问题是解答的关键．