题目内容
已知命题p:x2-8x-20>0,命题q:1-m≤x≤1+m2,¬p是q的充分而不必要条件,求实数m的取值范围.
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:结合不等式的性质,利用充分条件和必要条件的定义进行判断.
解答:
解:由x2-8x-20>0得x>10或x<-2,即¬p:-2≤x≤10,
若¬p是q的充分而不必要条件,
则¬p⇒q,
则
且等号不能同时取得,
∴
,解得m≥3,
当m=3时,q:-2≤x≤10,此时不成立.
∴m>3.
故实数m的取值范围是(3,+∞).
若¬p是q的充分而不必要条件,
则¬p⇒q,
则
|
∴
|
当m=3时,q:-2≤x≤10,此时不成立.
∴m>3.
故实数m的取值范围是(3,+∞).
点评:本题主要考查充分条件和必要条件的应用,利用不等式的解法是解决本题的关键,比较基础.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
下列所示各函数中,为奇函数的是( )
A、f(x)=
| ||
| B、f(x)=log2x | ||
| C、f(x)=2x | ||
| D、f(x)=x2 |
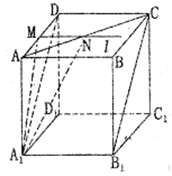 在长方体ABCD-A1B1C1D1中,AB=
在长方体ABCD-A1B1C1D1中,AB=