题目内容
16.已知数列{an}是首项为1,公差为2m的等差数列,前n项和为Sn,设bn=$\frac{{S}_{n}}{n•{2}^{n}}$(n∈N*),若数列{bn}是递减数列,则实数m的取值范围是[0,1).分析 利用求和公式可得Sn=n+$\frac{n(n-1)}{2}$×2m.可得bn=$\frac{{S}_{n}}{n•{2}^{n}}$=$\frac{mn+1-m}{{2}^{n}}$,由数列{bn}是递减数列,可得bn+1<bn,即可得出.
解答 解:Sn=n+$\frac{n(n-1)}{2}$×2m=mn2+(1-m)n.
∴bn=$\frac{{S}_{n}}{n•{2}^{n}}$=$\frac{mn+1-m}{{2}^{n}}$,
∵数列{bn}是递减数列,
∴bn+1<bn,∴$\frac{(n+1)m+1-m}{{2}^{n+1}}$<$\frac{mn+1-m}{{2}^{n}}$,
化为:m(n-2)+1>0,对于?n∈N*都成立.
n=1时,m<1;
n=2时,m∈R;
n>2时,m$>\frac{1}{2-n}$,解得m≥0.
综上可得:m∈[0,1).
故答案为:[0,1).
点评 本题考查了等差数列的求和公式、不等式的解法、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.若a<b<0,则下列不等式关系中,不能成立的是( )
| A. | $\frac{1}{a}$$>\frac{1}{b}$ | B. | $\frac{1}{a-b}$$>\frac{1}{a}$ | C. | a${\;}^{\frac{1}{3}}$$<{b}^{\frac{1}{3}}$ | D. | a2>b2 |
1.奇函数f(x)在区间[3,6]上是增函数,在区间[3,6]上的最大值为8,最小值为-1,则f(6)+f(-3)的值为( )
| A. | 10 | B. | -10 | C. | 9 | D. | 15 |
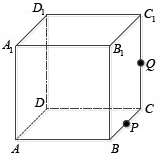 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是①③④⑤(写出所有正确命题的编号).
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是①③④⑤(写出所有正确命题的编号).