题目内容
17.已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),当0≤x≤1时,f(x)=x2,则f(2015)=-1.分析 根据已知可得f(x)是周期为4的周期函数,故f(2015)=f(-1)=-f(1),进而得到答案.
解答 解:∵f(x+2)=-f(x),
∴f(x+4)=f[(x+2)+2]=-f(x+2)=f(x),
即f(x)是周期为4的周期函数,
∴f(2015)=f(-1)=-f(1),
又∵当0≤x≤1时,f(x)=x2,
∴f(1)=1,
∴f(2015)=-1,
故答案为:-1
点评 本题考查的知识点是函数奇偶性的性质,熟练掌握函数奇偶性的性质,是解答的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
7.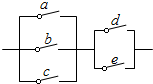 如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )
如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )
 如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )
如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{20}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{10}$ |
2.已知向量$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(2m,1),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则m的值为( )
| A. | -1 | B. | 1 | C. | $-\frac{1}{4}$ | D. | $\frac{1}{4}$ |
9.直线l1:2x-y-1=0与直线l2:mx+4y+2=0互相平行的充要条件是( )
| A. | m=-8 | B. | $m=-\frac{1}{2}$ | C. | m=8 | D. | m=2 |