题目内容
已知a∈R,函数f(x)=(-x2+ax)ex(x∈R,e为自然对数的底数).问函数f(x)是否为R上的单调递减函数?若是,求出a的取值范围;若不是,请说明理由.
考点:函数单调性的性质
专题:导数的综合应用
分析:求函数的导数,判断f'(x)≤0是否成立即可得到结论.
解答:
解:∵f(x)=(-x2+ax)ex,
∴f'(x)=[-x2+(a-2)x+a]ex,
要使函数f(x)是否为R上的单调递减函数,
则f'(x)=[-x2+(a-2)x+a]ex≤0,
即-x2+(a-2)x+a≤0,
∴x2-(a-2)x-a≥0恒成立,
∴△=(a-2)2+4a2≤0,
∴5a2-4a+4≤0,
∵△1=16-4×5×4=-64<0,
∴5a2-4a+4≤0不成立,
即函数f(x)在R上的不可能是单调递减函数.
∴f'(x)=[-x2+(a-2)x+a]ex,
要使函数f(x)是否为R上的单调递减函数,
则f'(x)=[-x2+(a-2)x+a]ex≤0,
即-x2+(a-2)x+a≤0,
∴x2-(a-2)x-a≥0恒成立,
∴△=(a-2)2+4a2≤0,
∴5a2-4a+4≤0,
∵△1=16-4×5×4=-64<0,
∴5a2-4a+4≤0不成立,
即函数f(x)在R上的不可能是单调递减函数.
点评:本题主要考查函数单调性的判断,利用导数是解决本题的关键,要求熟练掌握一元二次不等式的解法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设i为虚数单位,则复数
等于( )
| 3-4i |
| i |
| A、4+3i | B、4-3i |
| C、-4+3i | D、-4-3i |
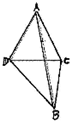 如图所示,某炮兵阵地位于点A处,两处观察所分别位于点D和C处,已知△ADC为正三角形,且DC=a,当目标在B点出现时,测量∠CDB=45°,∠BCD=75°,则炮兵阵地与目标的距离AB是多少?
如图所示,某炮兵阵地位于点A处,两处观察所分别位于点D和C处,已知△ADC为正三角形,且DC=a,当目标在B点出现时,测量∠CDB=45°,∠BCD=75°,则炮兵阵地与目标的距离AB是多少?