题目内容
盒中装有16个球,其中6个是玻璃球,10个是木质球.玻璃球中有2个是红色的,4个是蓝色的;木质球中有3个是红色的,7个是蓝色的.
(1)现从中任取1个,已知取到的是蓝球,问该球是玻璃球的概率是多少?
(2)现从中任取1个,取后放回,则第一次取到的是蓝球且第二次取得的是玻璃球的概率是多少?
(1)现从中任取1个,已知取到的是蓝球,问该球是玻璃球的概率是多少?
(2)现从中任取1个,取后放回,则第一次取到的是蓝球且第二次取得的是玻璃球的概率是多少?
考点:互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)求出任取一个球是蓝球的概率,再求出任取一个球为蓝色的玻璃球的概率,然后直接由条件概率公式求解;
(2)第一次取到的是蓝球和第二次取得的是玻璃球相互独立,直接由相互独立事件的概率乘法公式求解.
(2)第一次取到的是蓝球和第二次取得的是玻璃球相互独立,直接由相互独立事件的概率乘法公式求解.
解答:
解:(1)令事件A为任取一个球是蓝球,令事件B为任取一个球为玻璃球,
则事件AB为任取一个球为蓝色的玻璃球.
由题意可知P(A)=
=
,P(AB)=
,∴P(B|A)=
=
=
.
(2)记C为第一次取到的是蓝球,D为第二次取得的是玻璃球,
则C与D相互独立,且P(C)=
,P(D)=
=
,
∴P(CD)=P(C)P(D)=
•
=
.
则事件AB为任取一个球为蓝色的玻璃球.
由题意可知P(A)=
| 4+7 |
| 16 |
| 11 |
| 16 |
| 4 |
| 16 |
| P(AB) |
| P(A) |
| ||
|
| 4 |
| 11 |
(2)记C为第一次取到的是蓝球,D为第二次取得的是玻璃球,
则C与D相互独立,且P(C)=
| 11 |
| 16 |
| 6 |
| 16 |
| 3 |
| 8 |
∴P(CD)=P(C)P(D)=
| 11 |
| 16 |
| 3 |
| 8 |
| 33 |
| 128 |
点评:本题考查了互斥事件的概率加法公式与相互独立事件的概率乘法公式,关键是对题意的理解,是基础题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
已知某几何体的三视图(单位:cm)如图所示,则此几何体的体积是( )


| A、1cm3 |
| B、3cm3 |
| C、5cm3 |
| D、7cm3 |
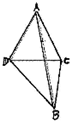 如图所示,某炮兵阵地位于点A处,两处观察所分别位于点D和C处,已知△ADC为正三角形,且DC=a,当目标在B点出现时,测量∠CDB=45°,∠BCD=75°,则炮兵阵地与目标的距离AB是多少?
如图所示,某炮兵阵地位于点A处,两处观察所分别位于点D和C处,已知△ADC为正三角形,且DC=a,当目标在B点出现时,测量∠CDB=45°,∠BCD=75°,则炮兵阵地与目标的距离AB是多少?