题目内容
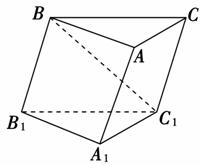
如图,在四棱柱ABCDA1B1C1D1中,已知底面ABCD是边长为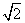 的正方形,侧棱D1D垂直于底面ABCD,且D1D=3.
的正方形,侧棱D1D垂直于底面ABCD,且D1D=3.
(1)点P在侧棱C1C上,若CP =1,求证:A1P⊥平面PBD;
=1,求证:A1P⊥平面PBD;
(2)求三棱锥A1-BDC1的体积V.

(1)证明:依题意,CP=1,C1P=2,在Rt△BCP中,PB= =
= ,
,
同理可知 ,A1P=
,A1P= =2
=2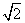 ,
,
A1B= =
= ,
,
所以A1P2+PB2=A1B2,则A1P⊥PB,
同理可证,A1P⊥PD,
由于PB∩PD=P,PB⊂平面 PBD,PD⊂平面PBD,
PBD,PD⊂平面PBD,
所以,A1P⊥平面PBD.
(2)解析:如图,易知三棱锥A1BDC1的体积等于四棱柱的体积减去四个体积相等的三棱锥的体积,
即VA1-BDC1=VABCD-A1B1C1D1-4VA1-ABD
=AB×AD×A1A-4× ×
× ×A1A
×A1A
= ×
×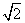 ×
×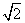 ×3=2.
×3=2.

练习册系列答案
相关题目
 ,集合
,集合 ,
, ,则
,则 ( )
( ) B.
B.  C.
C.  D.
D. 
 在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上是
在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上是


 D.
D.
 序号是( )
序号是( )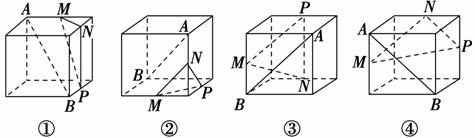
 C.②③ D.②④
C.②③ D.②④ 的单调递增区间为________.
的单调递增区间为________.