题目内容

15．若函数y=f（x）在x=2处的导数为-2，则$\underset{lim}{x→2}$$\frac{f（x）-f（2）}{x-2}$（　　）
A．-1B．-2C．2D．1

分析 直接利用导数的定义f′（x ），即可求得．

解答 解：∵函数y=f（x）在x=2处的导数为-2，
∴$\underset{lim}{x→2}$$\frac{f（x）-f（2）}{x-2}$=f′（2）=-2，
故选：B．

点评 本题主要考查了导数的定义，以及极限及其运算，属于基础题．

练习册系列答案
相关题目
5．下列四种说法：
①垂直于同一平面的所有向量一定共面；
②在△ABC中，已知$\frac{cosA}{a}=\frac{cosB}{b}=\frac{cosC}{c}$，则∠A=60°；
③在△ABC中，sin2A=sin2B+sin2C+sinBsinC，则A=$\frac{π}{3}$
④若a＞0，b＞0，a+b=2，则a2+b2≥2；
正确的序号有①②④．
6．已知函数y=ax+2-2（a＞0且a≠1）的图象恒过定点A，若点A在直线mx+ny+1=0上，其中mn＞0，则当$\frac{1}{m}$+$\frac{1}{n}$取最小值时，椭圆$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1的离心率为$\frac{\sqrt{2}}{2}$．
3．已知sinα，cosα是方程x2+ax+2b2=0的两个根，且0≤α＜2π，a，b为整数，求角α
10．求下列函数的导数：
（1）y=x-sin$\frac{x}{2}$cos$\frac{x}{2}$；
（2）y=sin4$\frac{x}{4}$+cos4$\frac{x}{4}$；
（3）y=$\frac{1+\sqrt{x}}{1-\sqrt{x}}$+$\frac{1-\sqrt{x}}{1+\sqrt{x}}$；
（4）y=-sin$\frac{x}{2}$（1-2cos2$\frac{x}{4}$）．
20．已知M（a，b）是圆O：x2+y2=r2内不在坐标轴上的一点，直线l的方程为ax+by=r2，直线m被圆O所截得的弦的中点为M，则下列说法中正确的是（　　）
A．m∥l且l与圆O相交B．m⊥l且l与圆O相切C．m∥l且l与圆O相离D．m⊥l且l与圆O相离
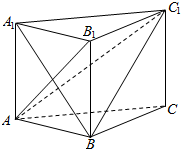7．化简：$\frac{1+sin2θ-cos2θ}{1+sin2θ+cos2θ}$+$\frac{1+sin2θ+cos2θ}{1+sin2θ-cos2θ}$．
4．函数f（x）=a•lnx在点（1，0）处的切线方程是y=2x+b，求a，b．
13．如图，三棱柱中ABC-A1B1C1，侧棱与底面ABC垂直，且AB1⊥BC1，AB=AA1=1，BC=2．
（I）证明：AB1⊥A1C1；
（Ⅱ）求点A1到平面ABC1的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网