题目内容
20．已知M（a，b）是圆O：x2+y2=r2内不在坐标轴上的一点，直线l的方程为ax+by=r2，直线m被圆O所截得的弦的中点为M，则下列说法中正确的是（ ）| A． | m∥l且l与圆O相交 | B． | m⊥l且l与圆O相切 | C． | m∥l且l与圆O相离 | D． | m⊥l且l与圆O相离 |
分析 求圆心到直线的距离，然后与a2+b2＜r2比较，可以判断直线与圆的位置关系，易得两直线的关系．
解答 解：以点M为中点的弦所在的直线的斜率是-$\frac{a}{b}$，直线m∥l，点M（a，b）是圆x2+y2=r2内一点，所以a2+b2＜r2，圆心到ax+by=r2，距离是$\frac{{r}^{2}}{\sqrt{{a}^{2}+{b}^{2}}}$＞r，故相离．
故选：C．
点评 本题考查直线与圆的位置关系，两条直线的位置关系，是基础题．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
8．已知点P（t，$\sqrt{3}$）为锐角φ终边上的一点，且cosφ=$\frac{t}{2}$，若函数f（x）=2sin（ωx+φ）（ω＞0）的图象与直线y=2相邻的两交点之间的距离为π，则函数f（x）的一条对称轴为（ ）
| A． | x=$\frac{π}{12}$ | B． | x=$\frac{π}{6}$ | C． | x=$\frac{π}{3}$ | D． | x=$\frac{π}{2}$ |
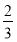x＋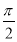
）是奇函数；
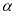，使得sin
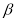是第一象限角且
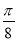是函数y＝sin（2x＋
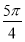）的一条对称轴方程；
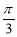）的图象关于点（
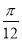，0）成中心对称图形．