题目内容
4.函数f(x)=a•lnx在点(1,0)处的切线方程是y=2x+b,求a,b.分析 求出函数的导数后代入求出f′(1),即为所求的切线斜率,再代入点斜式进行整理得到切线方程,即可求a,b.
解答 解:由f′(x)=(alnx)′=$\frac{a}{x}$,得在点x=1处的切线斜率k=f′(1)=a,
∴在点x=1处的切线方程为:y=a(x-1)=ax-a,
∵函数f(x)=a•lnx在点(1,0)处的切线方程是y=2x+b,
∴a=2,b=-a=-2.
点评 本题考查了导数的几何意义和直线点斜式方程,关键求出某点处切线的斜率即该点处的导数值,还有切点的坐标,利用切点在曲线上和切线上.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
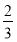 x+
x+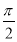 )是奇函数;
)是奇函数;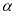 ,使得sin
,使得sin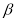 是第一象限角且
是第一象限角且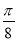 是函数y=sin(2x+
是函数y=sin(2x+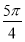 )的一条对称轴方程;
)的一条对称轴方程;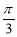 )的图象关于点(
)的图象关于点(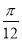 ,0)成中心对称图形.
,0)成中心对称图形.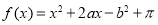 有零点的概率为( )
有零点的概率为( )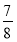 B.
B. 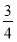 C.
C. 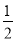 D.
D. 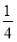
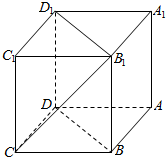 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别是AB、AD、AA1的中点,
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别是AB、AD、AA1的中点,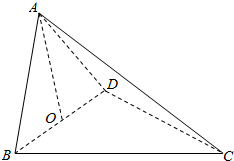 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=$\sqrt{6}$.
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=$\sqrt{6}$.