题目内容
6.已知函数y=ax+2-2(a>0且a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中mn>0,则当$\frac{1}{m}$+$\frac{1}{n}$取最小值时,椭圆$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1的离心率为$\frac{\sqrt{2}}{2}$.分析 由已知求出A的坐标,代入直线mx+ny+1=0,可得2m+n=1,求出$\frac{1}{m}$+$\frac{1}{n}$取最小值时m,n的值,结合隐含条件求出椭圆的半焦距,代入离心率公式得答案.
解答 解:∵y=ax(a>0且a≠1)的图象恒过定点(0,1),
∴函数y=ax+2-2(a>0且a≠1)的图象恒过定点A(-2,-1),
由点A在直线mx+ny+1=0上,得-2m-n+1=0,
∴2m+n=1,
则$\frac{1}{m}$+$\frac{1}{n}$=($\frac{1}{m}$+$\frac{1}{n}$)(2m+n)=3+$\frac{n}{m}+\frac{2m}{n}$,
∵mn>0,
∴$\frac{1}{m}$+$\frac{1}{n}$=3+$\frac{n}{m}+\frac{2m}{n}$$≥3\sqrt{\frac{n}{m}•\frac{2m}{n}}=3\sqrt{2}$.
当且仅当$\left\{\begin{array}{l}{2m+n=1}\\{\frac{n}{m}=\frac{2m}{n}}\end{array}\right.$,即m=1-$\frac{\sqrt{2}}{2}$,n=$\sqrt{2}-1$时上式等号成立.
∴${a}^{2}={n}^{2}=(\sqrt{2}-1)^{2}=3-2\sqrt{2}$,${c}^{2}={a}^{2}-{b}^{2}=(\sqrt{2}-1)^{2}-(1-\frac{\sqrt{2}}{2})^{2}$=$\frac{3}{2}-\sqrt{2}$,
则${e}^{2}=\frac{{c}^{2}}{{a}^{2}}=\frac{\frac{1}{2}(3-2\sqrt{2})}{3-2\sqrt{2}}=\frac{1}{2}$,
∴e=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查椭圆的简单性质,考查了利用基本不等式求最值,考查椭圆的标准方程,训练了利用椭圆标准方程求椭圆离心率的方法,是中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案| A. | 5x-5y-4=0 | B. | 5x-5y+4=0. | C. | 5x+5y-4=0 | D. | 3x+5y-4=0 |
(1)求函数F(x)=f(x)f(-x)+f2(x)的单调递增区间;
(2)设△ABC的三边a,b,c满足b2=ac,且边b所对的角为B,求函数f(B)的值域.
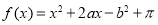 有零点的概率为( )
有零点的概率为( )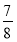 B.
B. 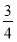 C.
C.  D.
D.