题目内容
已知直线l过点O（0，0）且与圆C：（x-2）2+y2=3有公共点，则直线l的斜率最大值为 ．
考点：直线与圆的位置关系,直线的斜率
专题：计算题,直线与圆
分析：设直线方程为y=kx，代入圆C：（x-2）2+y2=3消y并整理得（1+k2）x2-4x+1=0，由△≥0解不等式可得．
解答：
解：设直线l的斜率为k，则方程为y=kx，
代入圆C：（x-2）2+y2=3消y并整理得（1+k2）x2-4x+1=0，
由题意可得△=（-4）2-4（1+k2）≥0，解得-
≤k≤
，
所以直线l的斜率最大值为
．
故答案为：
．
代入圆C：（x-2）2+y2=3消y并整理得（1+k2）x2-4x+1=0，
由题意可得△=（-4）2-4（1+k2）≥0，解得-
| 3 |
| 3 |
所以直线l的斜率最大值为
| 3 |
故答案为：
| 3 |
点评：本题考查直线与圆的位置关系，涉及直线的斜率和一元二次不等式的解法，属基础题．
练习册系列答案
相关题目
已知集合A={y|y=x2-2x+2，-1≤x≤2}，B={x|
＞1}}，若任取x∈A，则x∈A∩B的概率为（ ）
| 2x-7 |
| x-3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
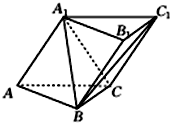如图，三棱柱ABC-A1B1C1中，侧面AA1C1C⊥底面ABC，AA1=A1C=AC=2，AB=BC且AB⊥BC．函数y=
的图象大致是（ ）
| x2 |
| ln|x| |
A、 |
B、 |
C、 |
D、 |
同时抛掷三枚均匀的硬币，均为正面向上的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|