题目内容
设函数f(x)=x|x-2|,则当x∈(0,2)时,函数f(x)的最大值等于 ,若x0是函数g(x)=f(f(x))-1的所有零点中的最大值,且x0∈(k,k+1)(k∈Z),则k= .
考点:函数的最值及其几何意义,函数零点的判定定理
专题:计算题,作图题,函数的性质及应用
分析:当x∈(0,2)时,配方法求最值;作函数的图象,故可得f(x0)=1+
,从而由零点的判定定理判断位置.
| 2 |
解答:
解:当x∈(0,2)时,
f(x)=x|x-2|=x(2-x)=-(x-1)2+1≤1;
作函数f(x)=x|x-2|的图象如下,
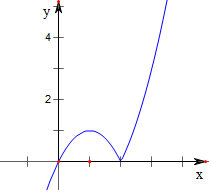
解x|x-2|=1得,
x=1或x=1+
;
又∵x0是函数g(x)=f(f(x))-1的所有零点中的最大值,
∴f(x0)=1+
;
且f(2)=0<1+
,f(3)=3>1+
;
故k=2.
故答案为:1,2.
f(x)=x|x-2|=x(2-x)=-(x-1)2+1≤1;
作函数f(x)=x|x-2|的图象如下,

解x|x-2|=1得,
x=1或x=1+
| 2 |
又∵x0是函数g(x)=f(f(x))-1的所有零点中的最大值,
∴f(x0)=1+
| 2 |
且f(2)=0<1+
| 2 |
| 2 |
故k=2.
故答案为:1,2.
点评:本题考查了复合函数的性质应用及数形结合的思想应用,属于中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
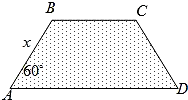 某地区要建造一条防洪堤,其横断面为等腰梯形(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为9
某地区要建造一条防洪堤,其横断面为等腰梯形(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为9| 3 |
| 3 |
| A、[3,5] |
| B、(3,5) |
| C、(2,6] |
| D、[2,6) |
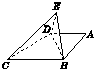 如图,在直角梯形ABCD中,AD∥BC,AD=AB,∠A=90°,BD⊥DC,将△ABD沿BD折起到△EBD的位置,使平面EBD⊥平面BDC.
如图,在直角梯形ABCD中,AD∥BC,AD=AB,∠A=90°,BD⊥DC,将△ABD沿BD折起到△EBD的位置,使平面EBD⊥平面BDC.




