题目内容
2.已知$\frac{tanα+1}{tanα-1}$=2,则cos2α=( )| A. | -$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
分析 由已知即可解得tanα的值,然后利用同角三角函数基本关系式,二倍角公式化简所求即可计算求值.
解答 解:∵$\frac{tanα+1}{tanα-1}$=2,
∴解得:tanα=3,
∴cos2α=$\frac{co{s}^{2}α-si{n}^{2}α}{co{s}^{2}α+si{n}^{2}α}$=$\frac{1-ta{n}^{2}α}{1+ta{n}^{2}α}$=$\frac{1-9}{1+9}$=-$\frac{4}{5}$.
故选:C.
点评 本题主要考查了同角三角函数基本关系式,二倍角公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
17.角-330°的终边所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.已知i2=-1,复数z=i(1-i),则|z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{3}$ |
14.已知角α的终边过点P(-4,-6sin150°),则sin2α的值为( )
| A. | -$\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{12}{25}$ | D. | $\frac{24}{25}$ |
11.已知函数y=ax2+bx+c,其中a,b,c∈{0,1,2,3,4},则不同的二次函数的个数共有( )
| A. | 125 | B. | 15 | C. | 100 | D. | 10 |
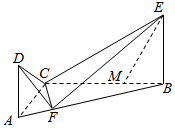 如图,直角三角形ABC中,∠BAC=60°,点F在斜边AB上,且AB=4AF.D,E是平面ABC同一侧的两点,AD⊥平面ABC,BE⊥平面ABC,AD=3,AC=BE=4.
如图,直角三角形ABC中,∠BAC=60°,点F在斜边AB上,且AB=4AF.D,E是平面ABC同一侧的两点,AD⊥平面ABC,BE⊥平面ABC,AD=3,AC=BE=4.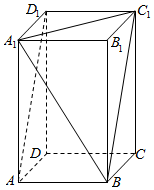 在长方体ABCD-A1B1C1D1中,AB=$\sqrt{2}$,BC=1,AA1=$\sqrt{3}$
在长方体ABCD-A1B1C1D1中,AB=$\sqrt{2}$,BC=1,AA1=$\sqrt{3}$