题目内容
函数y=3x与y=-3-x的图象的对称图形为( )
| A、x轴 | B、y轴 |
| C、直线y=x | D、原点 |
考点:函数的图象与图象变化
专题:函数的性质及应用
分析:在函数y=3x的图象上任取一点A(a,3a),可得A关于原点的对称点A′恰好在y=-3-x的图象上,由此可得两函数的图象关于原点对称,得到本题的答案.
解答:
解:在函数y=3x的图象上取一点A(a,3a),
可得点A对应函数y=-3-x图象上的点A′(-a,-3a),
∵A与A′关于原点对称,
∴由点A的任意性,得函数y=3x与y=-3-x的图象关于原点对称,
故选D.
可得点A对应函数y=-3-x图象上的点A′(-a,-3a),
∵A与A′关于原点对称,
∴由点A的任意性,得函数y=3x与y=-3-x的图象关于原点对称,
故选D.
点评:本题给出两个指数函数的图象,求它们关于哪种图形对称,着重考查了指数函数的图象与性质和图象对称等知识,属于基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
直线x=tan60°的倾斜角是( )
| A、90° | B、60° |
| C、30° | D、没有倾斜角 |
等比数列{an}的各项均为正数,且a2a9=9,数列{bn}满足bn=log3an,则数列{bn}前10项和为( )
| A、10 |
| B、12 |
| C、8 |
| D、2+log35 |
若原点在圆(x-1)2+(y+2)2=m的内部,则实数m的取值范围是( )
| A、m>5 | B、m<5 |
| C、-2<m<2 | D、0<m<2 |
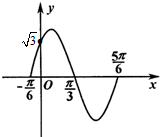 函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<
函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<