题目内容
19.将函数y=2sin(2x+$\frac{π}{3}$)的图象向右平移$\frac{π}{2}$个单位,所得图象对应的函数( )| A. | 在区间[$\frac{π}{12}$,$\frac{7π}{12}$]上单调递增 | B. | 在区间[$\frac{π}{12}$,$\frac{7π}{12}$]上单调递减 | ||
| C. | 在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递增 | D. | 在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递减 |
分析 利用函数y=Asin(ωx+φ)的图象变换规律求得所得图象对应的解析式,再利用正弦函数的单调性,求得所得图象对应的函数的单调区间,即可得解.
解答 解:将函数y=2sin(2x+$\frac{π}{3}$)的图象向右平移$\frac{π}{2}$个单位长度,
得到y=2sin[2(x-$\frac{π}{2}$)+$\frac{π}{3}$]=2sin(2x-$\frac{2π}{3}$)的图象,
令2kπ-$\frac{π}{2}$≤2x-$\frac{2π}{3}$≤2kπ+$\frac{π}{2}$,得kπ+$\frac{π}{12}$≤x≤kπ+$\frac{7π}{12}$,k∈Z,
可得函数的单调递增区间为:[kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}$],k∈Z,
当k=0时,单调递增区间为:[$\frac{π}{12}$,$\frac{7π}{12}$],故A正确.
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性,属于基础题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
14.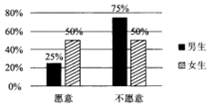 2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
(1)根据条件完成下列2×2列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
(2)现用分层抽样的方法从愿意接受挑战的市民中选取7名挑战者,再从中抽取2人参加挑战,求抽取的2人中至少有一名男生的概率.
参考公式与数据:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
 2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:(1)根据条件完成下列2×2列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
| 愿意 | 不愿意 | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 |
参考公式与数据:
| P(K2≥k0) | 0.1 | 0.05 | 0.025 | 0.01 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
11.将一根长为3米的绳子在任意位置剪断,则剪得两段的长度都不小于1米的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
8.点P在双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右支上,其左右焦点分别为F1,F2,直线PF1与以坐标原点O为圆心a为半径的圆相切于点A,线段PF1的垂直平分线恰好过点F2,则$\frac{{S}_{△O{F}_{2}A}}{{S}_{△P{F}_{1}{F}_{2}}}$的值为( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |