题目内容
14.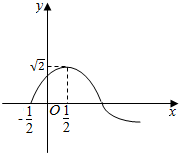 若函数f(x)=Asin(ωx+φ)(ω>0,A>0,0<φ<π)的部分图象如图所示,则f(0)+f(1)+f(2)+…+f(2008)=( )
若函数f(x)=Asin(ωx+φ)(ω>0,A>0,0<φ<π)的部分图象如图所示,则f(0)+f(1)+f(2)+…+f(2008)=( )| A. | 0 | B. | 1 | C. | 2 | D. | -1 |
分析 先由图象可知f(0)=f(1)=1,f(2)=f(3)=-1且周期为4,进而可得f(1)+f(2)+f(3)+f(0)=0进而利用周期性即可得解.
解答 解:由图可知:A=$\sqrt{2}$,函数f(x)的周期T=4×[$\frac{1}{2}-$(-$\frac{1}{2}$)]=4=$\frac{2π}{ω}$,ω>0,$ω=\frac{π}{2}$,
点($\frac{1}{2}$,$\sqrt{2}$)在函数图象上,可得:$\sqrt{2}$sin($\frac{π}{2}$×$\frac{1}{2}$+φ)=$\sqrt{2}$,解得:φ=2kπ+$\frac{π}{4}$,k∈Z,
又0<φ<π,可得:φ=$\frac{π}{4}$,
所以:f(x)=$\sqrt{2}$sin($\frac{π}{2}$x+$\frac{π}{4}$).
可得:f(0)=1
f(1)=1
f(2)=-1
f(3)=-1
f(4)=1
…
则f(0)+f(1)+f(2)+…+f(2008)=0+f(2008)=0+1=1.
故选:B.
点评 本题主要考查了函数y=Asin(ωx+φ)的图象,要理解好函数的中的周期、振幅、初相等概念.

练习册系列答案
相关题目
5.已知点A(0,1),动点P(x,y)的坐标满足y≤|x|,那么|PA|的最小值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
2.下列函数中,既是偶函数,又是(0,+∞)上单调递增的函数是( )
| A. | y=x3 | B. | y=|x|+1 | C. | y=-x2+1 | D. | y=x-2 |
6.设直线l1、l2的倾斜角分别为θ1、θ2,斜率分别为k1、k2.且θ1+θ2=90°,则k1+k2的最小值为( )
| A. | 2 | B. | -2 | C. | $\sqrt{2}$ | D. | 不存在 |
3.已知集合A={1,2,3,4,5},B={x∈R|x≥2},则∁A(A∩B)等于( )
| A. | {1} | B. | {0,1} | C. | {1,2} | D. | {0,1,2} |
17.已知i为虚数单位,则复数$\frac{2}{1-i}$所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 现将甲、乙两名学生的6次模拟测试成绩(百分制)制成如图所示的茎叶图:
现将甲、乙两名学生的6次模拟测试成绩(百分制)制成如图所示的茎叶图: