题目内容
6.设直线l1、l2的倾斜角分别为θ1、θ2,斜率分别为k1、k2.且θ1+θ2=90°,则k1+k2的最小值为( )| A. | 2 | B. | -2 | C. | $\sqrt{2}$ | D. | 不存在 |
分析 根据基本不等式的性质求出其最小值即可.
解答 解:∵k1=tanθ1,k2=tanθ2,<又θ1+θ2=90°所以 k2=$\frac{1}{ta{nθ}_{1}}$,
k1+k2=tanθ1+$\frac{1}{ta{nθ}_{1}}$≥2,
当tanθ1=1时等号取到,
故选:A.
点评 本题考察了三角函数问题,考察基本不等式的性质,是一道基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
17.已知集合A={x|0<log4x<1},B=$\left\{{x|y=\sqrt{1-{2^{x-3}}}}\right\}$,则A∩B=( )
| A. | (0,1) | B. | (0,3] | C. | (1,3) | D. | (1,3] |
1.已知二项式(2x+1)n的各项系数和为an,展开式x的系数为bn,设Cn=anbn,则数列{Cn}的前n项的和为Tn,则为T2014( )
| A. | 1+$\frac{4027}{2}$•32015 | B. | $\frac{3}{2}$+$\frac{4027}{2}$•32015 | C. | 1+$\frac{4027}{2}$•32014 | D. | $\frac{3}{2}$+$\frac{4027}{2}$•32014 |
11.设全集为R,集合M={y|y=$\sqrt{9-{x}^{2}}$},集合N={x|y=ln(x-x2+6)},则(∁RM)∪N=( )
| A. | {x|-2<x<0} | B. | {x|-2<x≤0} | C. | {x|x≠3} | D. | {x|x<0或x>2且x≠3} |
8.要得到函数y=cos(3x-$\frac{π}{4}$)的图象,只需将函数y=sin3x的图象( )
| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{12}$个单位 | ||
| C. | 向右平移$\frac{π}{4}$个单位 | D. | 向左平移$\frac{π}{4}$个单位 |
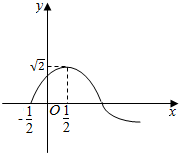 若函数f(x)=Asin(ωx+φ)(ω>0,A>0,0<φ<π)的部分图象如图所示,则f(0)+f(1)+f(2)+…+f(2008)=( )
若函数f(x)=Asin(ωx+φ)(ω>0,A>0,0<φ<π)的部分图象如图所示,则f(0)+f(1)+f(2)+…+f(2008)=( )