题目内容
9.求f(x)=a•2x-4x(a∈R)在[0,1]上的最大值.分析 设2x=t(1≤t≤2),即有g(t)=at-t2,求出对称轴方程,讨论区间[1,2]和对称轴的关系,运用单调性可得最大值.
解答 解:设2x=t(1≤t≤2),
即有g(t)=at-t2,
对称轴为t=$\frac{a}{2}$,
当$\frac{a}{2}$≥2时,即a≥4,区间[1,2]递增,
可得t=2即x=1时,取得最大值2a-4;
当1<$\frac{a}{2}$<2时,即2<a<4时,t=$\frac{a}{2}$时,即x=log2$\frac{a}{2}$,取得最大值$\frac{{a}^{2}}{4}$;
当$\frac{a}{2}$≤1时,即a≤2,区间[1,2]递减,
可得t=1即x=0时,取得最大值a-1.
综上可得,a≤2时,f(x)的最大值为a-1;
2<a<4时,f(x)的最大值为$\frac{{a}^{2}}{4}$;
a≥4时,f(x)的最大值为2a-4.
点评 本题考查可化为二次函数的最值的求法,注意讨论对称轴和区间的关系,考查运算能力,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
20.2015年9月3日,纪念中国人民抗日战争暨世界反法西斯战争胜利70周年大会在北京天安门广场隆重举行,大会中的阅兵活动向全世界展示了我军威武文明之师的良好形象,展示了科技强军的伟大成就以及维护世界和平的坚定决心,在阅兵活动的训练工作中,不仅使用了北斗导航、电子沙盘、仿真系统、激光测距机、迈速表和高清摄像头等新技术装备,还通过管理中心对每天产生的大数据进行存储、分析、有效保证了阅兵活动的顺利进行,假如训练过程过程中第一天产生的数据量为a,其后每天产生的数据量都是前一天的q(q>1)倍,那么训练n天产生的总数据量为( )
| A. | aqn-1 | B. | aqn | C. | $\frac{{a(1-{q^{n-1}})}}{1-q}$ | D. | $\frac{{a(1-{q^n})}}{1-q}$ |
17.已知集合A={x|0<log4x<1},B=$\left\{{x|y=\sqrt{1-{2^{x-3}}}}\right\}$,则A∩B=( )
| A. | (0,1) | B. | (0,3] | C. | (1,3) | D. | (1,3] |
1.已知二项式(2x+1)n的各项系数和为an,展开式x的系数为bn,设Cn=anbn,则数列{Cn}的前n项的和为Tn,则为T2014( )
| A. | 1+$\frac{4027}{2}$•32015 | B. | $\frac{3}{2}$+$\frac{4027}{2}$•32015 | C. | 1+$\frac{4027}{2}$•32014 | D. | $\frac{3}{2}$+$\frac{4027}{2}$•32014 |
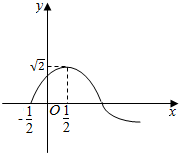 若函数f(x)=Asin(ωx+φ)(ω>0,A>0,0<φ<π)的部分图象如图所示,则f(0)+f(1)+f(2)+…+f(2008)=( )
若函数f(x)=Asin(ωx+φ)(ω>0,A>0,0<φ<π)的部分图象如图所示,则f(0)+f(1)+f(2)+…+f(2008)=( )