题目内容
13．实数x，y满足$\frac{x^2}{4}+\frac{y^2}{3}=1$，则2x+$\sqrt{3}$y的最大值是5．分析 由柯西不等式得（$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$）（42+32）$≥（\frac{x}{2}•4+\frac{y}{\sqrt{3}}•3）^{2}$=（2x+$\sqrt{3}y$）2，即可得2x+$\sqrt{3}$y的最大值，
解答 解：由柯西不等式得（$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$）（42+32）$≥（\frac{x}{2}•4+\frac{y}{\sqrt{3}}•3）^{2}$=（2x+$\sqrt{3}y$）2，
∴1×25$≥（2x+\sqrt{3}y）^{2}$，∴$2x+\sqrt{3}y≤5$，即2x+$\sqrt{3}$y的最大值是5，
故答案为：5．
点评 本题考查了柯西不等式的应用，属于基础题．
练习册系列答案
相关题目
8．函数$y=sin（x+\frac{π}{4}）$在闭区间（ ）上为增函数．
| A． | $[-\frac{3}{4}π，\frac{π}{4}]$ | B． | [-π，0] | C． | $[-\frac{π}{4}，\frac{3}{4}π]$ | D． | $[-\frac{π}{2}，\frac{π}{2}]$ |
18．已知2-9，2a1，2a2，2-1成等比数列，2，log3b1，log3b2，log3b3，0成等差数列，则b2（a2-a1）=（ ）
| A． | -8 | B． | 8 | C． | $-\frac{9}{8}$ | D． | $\frac{9}{8}$ |
5．设随机变量X的分布列为P（X=k）=$\frac{k}{25}$，k=1，2，3，4，5，则P（$\frac{1}{2}$＜X＜$\frac{5}{2}$）等于（ ）
| A． | $\frac{2}{15}$ | B． | $\frac{2}{5}$ | C． | $\frac{1}{5}$ | D． | $\frac{1}{15}$ |
2．
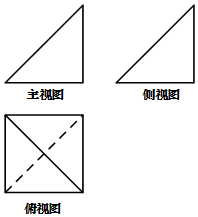某空间几何体的三视图如图所示，图中主视图和侧视图是两个全等的等腰直角三角形，腰长为4，俯视图中的四边形为正方形，则这个几何体的体积是（ ）
某空间几何体的三视图如图所示，图中主视图和侧视图是两个全等的等腰直角三角形，腰长为4，俯视图中的四边形为正方形，则这个几何体的体积是（ ）| A． | $\frac{32}{3}$ | B． | $\frac{64}{3}$ | C． | 16 | D． | 32 |