题目内容
已知不等式|a-3x|>x-1,对任意x∈[0,2]恒成立,则a的取值范围为 .
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:当x<1时,不等式恒成立,只需考虑x∈[1,2]的情况.当3x-a>0时,可得a<3;当3x-a≤0时,可得a>7.把2个实数a的取值范围取并集,即得所求.
解答:
解:当x<1时,x-1<0,|3x-a|>x-1恒成立,所以只考虑x∈[1,2]的情况.
当3x-a>0时,不等式即 3x-a>x-1,即 a<2x+1,可得a<3.
当3x-a≤0时,不等式即 a-3x>x-1,即a>4x-1,可得a>8-1=7.
所以,不等式恒成立时,实数a的取值范围是{a|a<3,或者a>7},
故答案为:{a|a<3,或者a>7}.
当3x-a>0时,不等式即 3x-a>x-1,即 a<2x+1,可得a<3.
当3x-a≤0时,不等式即 a-3x>x-1,即a>4x-1,可得a>8-1=7.
所以,不等式恒成立时,实数a的取值范围是{a|a<3,或者a>7},
故答案为:{a|a<3,或者a>7}.
点评:本题主要考查绝对值不等式的解法,函数的恒成立问题,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
已知某算法的流程图如图所示,则程序运行结束时输出的结果为( )

| A、10 | B、19 |
| C、-10 | D、-19 |
已知:两个非零向量
=(m-1,n-1),
=(m-3,n-3),且
与
的夹角是钝角或直角,则m+n的取值范围是( )
| a |
| b |
| a |
| b |
A、(
| ||||
| B、(2,6) | ||||
C、[
| ||||
| D、[2,6] |
已知平面向量
,
满足|
|=
,|
|=2,且(
-
)⊥
,则
与
的夹角为( )
| a |
| b |
| a |
| 3 |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f(x)=|ax+x2-xlna-t|-1(a>1)有三个零点,则t的值是( )
| A、2 | B、4 | C、8 | D、0 |
设
=(t,1)(t∈Z),
=(2,4),满足|
|≤4,则△OAB为直角三角形的概率是( )
| OA |
| OB |
| OA |
A、
| ||
B、
| ||
C、
| ||
D、
|
若如图的程序框图输出的S是126,则条件①可为( )


| A、n≤5 | B、n≤6 |
| C、n≤7 | D、n≤8 |
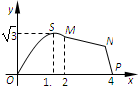 如图,某市拟在长为4km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0),X∈[0,2]的图象,且图象的最高点为S(
如图,某市拟在长为4km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0),X∈[0,2]的图象,且图象的最高点为S(