题目内容
给出下列命题:
①∀x∈R,不等式x2+2x>4x-3恒成立;
②若log2x+logx2≥2,则x>1;
③“若a>b>0且c<0,则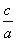 >
>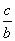 ”的逆否命题;
”的逆否命题;
④若命题p:∀x∈R,x2+1≥1,命题q:∃x∈R,x2-x-1≤0,则命题p∧綈q是真命题.
其中,真命题为________.(填序号)
①②③
解析 ①中不等式可表示为(x-1)2+2>0,恒成立;②中不等式可变为log2x+ ≥2,得x>1;③中由a>b>0,得
≥2,得x>1;③中由a>b>0,得 <
<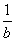 ,而c<0,所以原命题是真命题,则它的逆否命题也为真;④中綈q:∀x∈R,x2-x-1>0,由于x2-x-1=
,而c<0,所以原命题是真命题,则它的逆否命题也为真;④中綈q:∀x∈R,x2-x-1>0,由于x2-x-1=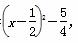 ,则存在x值使x2-x-1≤0,故綈q为假命题,则p∧綈q为假命题.
,则存在x值使x2-x-1≤0,故綈q为假命题,则p∧綈q为假命题.

练习册系列答案
相关题目
 若
若 = .
= . 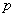 :函数
:函数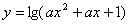 的定义域为
的定义域为 ,若
,若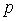 是真命题,则实数
是真命题,则实数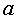 的取值范围_____________
的取值范围_____________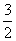 x-m=0在x∈[-1,1]上有实根,则m的取值范围是________.
x-m=0在x∈[-1,1]上有实根,则m的取值范围是________.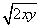 ≤λ(x+y)恒成立,则实数λ的最小值为________.
≤λ(x+y)恒成立,则实数λ的最小值为________.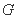 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,且经过点
轴上,且经过点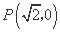 和点
和点 .
.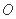 ,过直线
,过直线 上的动点
上的动点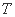 作圆
作圆 ,
, ,若直线
,若直线 与椭圆
与椭圆 ,
, ,求
,求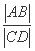 的取值范围.
的取值范围.