题目内容
已知椭圆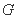 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,且经过点
轴上,且经过点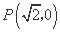 和点
和点 .
.
(Ⅰ)求椭圆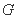 的标准方程;
的标准方程;
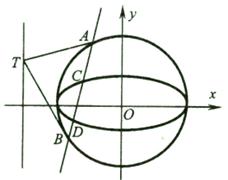
(Ⅱ)如图,以椭圆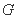 的长轴为直径作圆
的长轴为直径作圆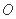 ,过直线
,过直线 上的动点
上的动点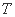 作圆
作圆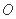 的两条切线,设切点分别为
的两条切线,设切点分别为 ,
, ,若直线
,若直线 与椭圆
与椭圆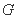 交于不同的两点
交于不同的两点 ,
, ,求
,求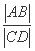 的取值范围.
的取值范围.
解:(Ⅰ)设椭圆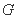 的标准方程为
的标准方程为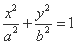 (
(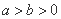 ),
),
将点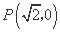 和点
和点 代入,得
代入,得
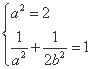 ,解得
,解得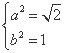 .
.
故椭圆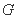 的标准方程为
的标准方程为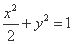 .
.
(Ⅱ)圆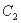 的标准方程为
的标准方程为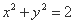 , 设
, 设 ,
,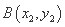 ,
,
则直线 的方程为
的方程为 ,直线
,直线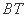 的方程为
的方程为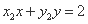 ,
,
再设直线 上的动点
上的动点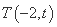 (
( ),由点
),由点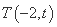 在直线
在直线 和
和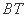 上,得
上,得
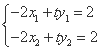 ,故直线
,故直线 的方程为
的方程为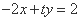 .
.
原点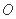 到直线
到直线 的距离
的距离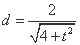 ,
,
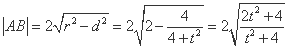 .
.
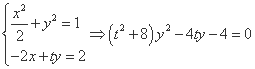 ,显然
,显然 .
.
设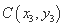 ,
,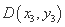 ,则
,则
 ,
,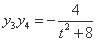 .
.
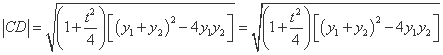
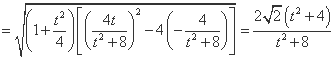 .
.
 .
.
设 (
(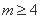 ),则
),则
 .
.
设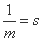 (
(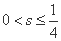 ),则
),则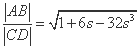 .
.
设 ,则
,则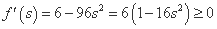 ,
,
故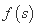 在
在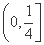 上为增函数,
上为增函数,
于是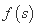 的值域为
的值域为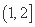 ,
,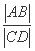 的取值范围是
的取值范围是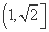 .
.

练习册系列答案
相关题目
下列函数中,既是偶函数又在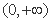 单调递增的函数是 ( )
单调递增的函数是 ( )
| (A) | (B) | (C) | (D) |
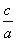 >
>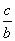 ”的逆否命题;
”的逆否命题;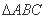 的外接圆的圆心为
的外接圆的圆心为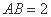 ,
, ,则
,则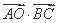 等于
等于 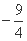 B.
B. C.
C. D.
D.
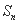 是等差数列
是等差数列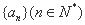 的前
的前 项和,且
项和,且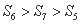 ,有下列五个命题:
,有下列五个命题: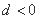 ;②
;② 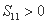 ;③
;③ 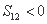 ;④ 数列
;④ 数列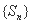 中的最大项为
中的最大项为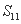 ;⑤
;⑤ 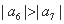 .
.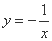
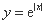
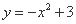
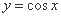
 的部分图像如图所示,则
的部分图像如图所示,则 的解析式可以为
的解析式可以为 B、
B、
 D、
D、


 的图像与
的图像与 轴相切于原点,当
轴相切于原点,当 ,求证:
,求证:
 上横坐标是2的点
上横坐标是2的点 到抛物线焦点距离是3,则
到抛物线焦点距离是3,则 ( )
( )