题目内容
给出以下命题:
①如果函数f(x)在区间(a,b)内可导,那么导数等于零的点一定是极值点;
②若复数z1,z2满足z1+z2,z1•z2都是实数,则z1,z2互为共轭复数;
③连续函数f(x)的图象与直线y=0,x=b(a<b)所围成的面积是
f(x)dx;
④反证法就是通过证明逆命题来证明原命题.
其中正确命题的个数是( )
①如果函数f(x)在区间(a,b)内可导,那么导数等于零的点一定是极值点;
②若复数z1,z2满足z1+z2,z1•z2都是实数,则z1,z2互为共轭复数;
③连续函数f(x)的图象与直线y=0,x=b(a<b)所围成的面积是
| ∫ | b a |
④反证法就是通过证明逆命题来证明原命题.
其中正确命题的个数是( )
| A、3 | B、2 | C、1 | D、0 |
考点:必要条件、充分条件与充要条件的判断
专题:应用题
分析:分别对①②③④进行判断,从而得到答案.
解答:
解:①错误,如y=x3在(a,b)内可导,
f′(x)=3x2=0,x=0,但x=0不是极值点,
故①错误;
②设z1=a+bi,z2=c+di,由z1+z2=a+c+(b+d)i是实数,得b=-d,
由z1•z2=(a+bi)(c+di)=ac+bd+(ad+bc)i是实数,
得ad+bc=0,即ad=bc,
∵b=-d,∴a=c,
∴z1,z2互为共轭复数,
故②正确;
③错误,如图示:
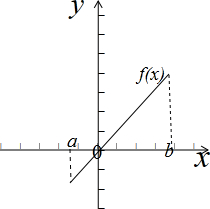 ,
,
则面积 应为S=
(-f(x))dx+
f(x)dx;
④错误,反证法是假设原命题结论正确,得出矛盾,而非证明逆命题;
故选:C.
f′(x)=3x2=0,x=0,但x=0不是极值点,
故①错误;
②设z1=a+bi,z2=c+di,由z1+z2=a+c+(b+d)i是实数,得b=-d,
由z1•z2=(a+bi)(c+di)=ac+bd+(ad+bc)i是实数,
得ad+bc=0,即ad=bc,
∵b=-d,∴a=c,
∴z1,z2互为共轭复数,
故②正确;
③错误,如图示:
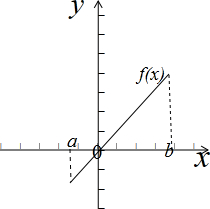 ,
,则面积 应为S=
| ∫ | 0 a |
| ∫ | b 0 |
④错误,反证法是假设原命题结论正确,得出矛盾,而非证明逆命题;
故选:C.
点评:本题考查了导数的问题,考查了复数问题,定积分以及反证法.

练习册系列答案
相关题目
复数=z=i3(1+i)(i为虚数单位)在复平面上对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
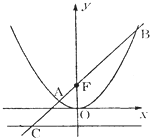 如图,过抛物线x2=2py (p>0)焦点F的直线l交抛物线于点A、B,交准线于点C,若|AC|=2|AF|,且|BF|=8,则此抛物线的方程为( )
如图,过抛物线x2=2py (p>0)焦点F的直线l交抛物线于点A、B,交准线于点C,若|AC|=2|AF|,且|BF|=8,则此抛物线的方程为( )| A、x2=4y |
| B、x2=8 y |
| C、x2=2y |
| D、x2=16y |
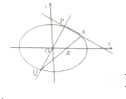 如图,已知y=kx(k≠0)与椭圆:
如图,已知y=kx(k≠0)与椭圆: