题目内容
已知|
|=1,|
|=
,且
⊥
,设
=m
+n
(1)若C点满足
=t
,求m+n的值;
(2)若C满足∠AOC=30°,求
的值.
| OA |
| OB |
| 3 |
| AO |
| OB |
| OC |
| OA |
| OB |
(1)若C点满足
| AC |
| CB |
(2)若C满足∠AOC=30°,求
| m |
| n |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:(1)根据题意,结合平面向量的线性运算,即可求出m+n的值;
(2)当∠AOC=30°时,画出图形,利用平面向量的平行四边形合成法则,求出
的值.
(2)当∠AOC=30°时,画出图形,利用平面向量的平行四边形合成法则,求出
| m |
| n |
解答:
解:(1)∵
=m
+n
,
=t
,
∴
-
=t(
-
),
∴(1+t)
=
+t
,
∴(1+t)(m
+n
)=
+t
;
∴
,
解得m=
,n=
,
∴m+n=
+
=1;
(2)当∠AOC=30°时,如图1,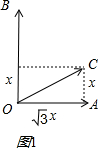
设AC=x,则OA=
x,
∴
x=1=m,
∴x=
;
∴n•
=
,
∴n=
;
∴
=
=3;
同理,当
、
、
的位置如图2所示时,
=-3.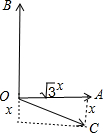
综上,
的值为3或-3.
| OC |
| OA |
| OB |
| AC |
| CB |
∴
| OC |
| OA |
| OB |
| OC |
∴(1+t)
| OC |
| OA |
| OB |
∴(1+t)(m
| OA |
| OB |
| OA |
| OB |
∴
|
解得m=
| 1 |
| 1+t |
| t |
| 1+t |
∴m+n=
| 1 |
| 1+t |
| t |
| 1+t |
(2)当∠AOC=30°时,如图1,
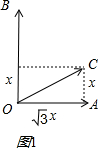
设AC=x,则OA=
| 3 |
∴
| 3 |
∴x=
| ||
| 3 |
∴n•
| 3 |
| ||
| 3 |
∴n=
| 1 |
| 3 |
∴
| m |
| n |
| 1 | ||
|
同理,当
| OA |
| OB |
| OC |
| m |
| n |

综上,
| m |
| n |
点评:本题考查了平面向量的应用问题,也考查了平面向量的线性运算与平面向量的基本定理的应用问题,是综合题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
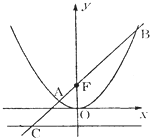 如图,过抛物线x2=2py (p>0)焦点F的直线l交抛物线于点A、B,交准线于点C,若|AC|=2|AF|,且|BF|=8,则此抛物线的方程为( )
如图,过抛物线x2=2py (p>0)焦点F的直线l交抛物线于点A、B,交准线于点C,若|AC|=2|AF|,且|BF|=8,则此抛物线的方程为( )| A、x2=4y |
| B、x2=8 y |
| C、x2=2y |
| D、x2=16y |
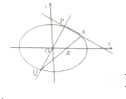 如图,已知y=kx(k≠0)与椭圆:
如图,已知y=kx(k≠0)与椭圆: