题目内容
关于函数f(x)=sin2x-(
)|x|+
有如下四个结论:①f(x)的图象关于y轴对称;②f(x)的值域是(-
,
);③当x∈(0,
)时,f(x)为增函数;④f(x)在R上有且只有一个零点,则正确结论的个数是( )
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| π |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
考点:函数的图象,函数零点的判定定理
专题:函数的性质及应用
分析:根据题意:依次分析命题:①运用f(-x)和f(x)关系,判定函数的奇偶性;②求出函数值域即可③利用导数求出函数的单调性④根据函数为偶函数和函数值域即可判断
解答:
解:y=f(x)的定义域为x∈R,且f(-x)=f(x),则函数f(x)为偶函数,故①正确.
因为f(x)=
(1-cos2x)-(
)|x|+
=1-
cos2x-(
)|x|,-1≤cos2x≤1,
所以-
≤1-
cos2x≤
,(
)|x|>0,
所以f(x)<
,
而cos2x,(
)|x|在x=0时同时取得最大值,
所以在x=0时可取的最小值-
,
故函数的值域为[-
,
),故②错误,
因为x∈(0,
)时,f(x)=
(1-cos2x)-(
)x+
,
所以f′(x)=sin2x-(
)xln
>0恒成立,
故当x∈(0,
)时,f(x)为增函数,故③正确,
由于函数为偶函数,且函数的值域为[-
,
),故f(x)在R上有且只有一个零点是错误的,故④错误
故选:B.
因为f(x)=
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
所以-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
所以f(x)<
| 3 |
| 2 |
而cos2x,(
| 2 |
| 3 |
所以在x=0时可取的最小值-
| 1 |
| 2 |
故函数的值域为[-
| 1 |
| 2 |
| 3 |
| 2 |
因为x∈(0,
| π |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
所以f′(x)=sin2x-(
| 2 |
| 3 |
| 2 |
| 3 |
故当x∈(0,
| π |
| 2 |
由于函数为偶函数,且函数的值域为[-
| 1 |
| 2 |
| 3 |
| 2 |
故选:B.
点评:本题以具体函数为载体,考查了函数奇偶性的判断及借助不等式知识对函数值域范围进行判断,涉及到函数奇偶性的判断,同时还涉及到三角函数、指数函数的范围问题,利用不等式的放缩求新函数的范围.综合性强

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
已知a=(
)
,b=log6
,c=log
,则a,b,c的大小关系是( )
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| A、a>b>c |
| B、c>a>b |
| C、a>c>b |
| D、c>b>a |
在一次歌咏比赛中,七位裁判为一选手打出的分数如下:
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
| A、92,2.8 |
| B、92,2 |
| C、93,2 |
| D、93,2.8 |
阅读如图所示的程序框图,则该算法的功能是( )
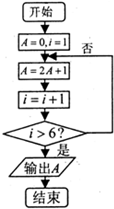

| A、计算数列{2n-1}前5项的和 |
| B、计算数列{2n-1}前5项的和 |
| C、计算数列{2n-1}前6项的和 |
| D、计算数列{2n-1}前6项的和 |
在平面直角坐标系中,直线(
-
)x+y=3和直线x+(
-
)y=2的位置关系是( )
| 3 |
| 2 |
| 2 |
| 3 |
| A、相互但不垂直 | B、平行 |
| C、垂直 | D、重合 |