题目内容
4．已知双曲线$\frac{x^2}{16}-\frac{y^2}{b^2}=1，（b＞0）$实轴的一端点为A，虚轴的一端点为B，且|AB|=5，则该双曲线的方程为（ ）| A． | $\frac{x^2}{16}-\frac{y^2}{15}=1$ | B． | $\frac{x^2}{16}-\frac{y^2}{12}=1$ | C． | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | D． | $\frac{x^2}{16}-\frac{y^2}{3}=1$ |
分析 求出双曲线实轴端点A与虚轴的一端点为B的坐标，利用距离求解即可．
解答 解：由题意不妨A（4，0），B（0，b），|AB|=5，
可得16+b2=25，解得b=3，
则该双曲线的方程为：$\frac{{x}^{2}}{16}-\frac{{y}^{2}}{9}=1$．
故选：C．
点评 本题考查双曲线的简单性质的应用，考查计算能力．
练习册系列答案
相关题目
9．
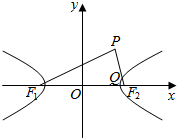如图，已知F1、F2为双曲线C：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a＞0，b＞0）的左、右焦点，点P在第一象限，且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$，（$\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$）•$\overrightarrow{{F}_{2}P}$=0，线段PF2与双曲线C交于点Q，若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$，则双曲线C的渐近线方程为（ ）
如图，已知F1、F2为双曲线C：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a＞0，b＞0）的左、右焦点，点P在第一象限，且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$，（$\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$）•$\overrightarrow{{F}_{2}P}$=0，线段PF2与双曲线C交于点Q，若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$，则双曲线C的渐近线方程为（ ）| A． | y=±$\frac{\sqrt{5}}{5}x$ | B． | y=±$\frac{1}{2}x$ | C． | y=±$\frac{\sqrt{3}}{2}x$ | D． | y=±$\frac{\sqrt{3}}{3}x$ |
16．圆锥的轴截面SAB是边长为4的正三角形（S为顶点），O为底面中心，M为SO中点，动点P在圆锥底面内（包括圆周），若AM⊥MP，则点P形成的轨迹长度为（ ）
| A． | $\frac{\sqrt{7}}{3}$ | B． | $\frac{\sqrt{7}}{2}$ | C． | $\frac{2}{5}\sqrt{7}$ | D． | $\sqrt{7}$ |
13．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，x＞0}\\{x+1，x≤0}\end{array}\right.$，则f（-2）=（ ）
| A． | -1 | B． | 0 | C． | $\frac{1}{4}$ | D． | 4 |
