题目内容
6.已知函数f(x)=$\left\{\begin{array}{l}{3^x},x≥0\\ 3x+1,x<0\end{array}\right.$,则不等式f(f(x))<4f(x)+1的解集是( )| A. | (-3,0) | B. | (-$\frac{1}{3}$,1) | C. | (0,2) | D. | (-$\frac{1}{3}$,log32) |
分析 根据分段函数的表达式,讨论f(x)的符号,将不等式进行转化求解即可.
解答 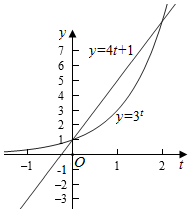 解:由3x+1=0得x=-$\frac{1}{3}$,
解:由3x+1=0得x=-$\frac{1}{3}$,
当x<-$\frac{1}{3}$时,3x+1<0,则由f(f(x))<4f(x)+1得f(3x+1))<4(3x+1)+1,
即3(3x+1)+1<12x+4+1,
即9x+4<12x+5,
得x>-$\frac{1}{3}$,此时不等式无解,
当x≥0时,f(x)=3x≥1,
则由f(f(x))<4f(x)+1得${3}^{{3}^{x}}$<4•3x+1,
设t=3x,
则不等式等价为3t<4t+1,
设g(t)=3t-4t-1,则g(0)=0,g(2)=9-8-1=0,
即g(t)<0的解为0<t<2,即0<3x<2,
得0≤x<log32,
当-$\frac{1}{3}$≤x<0时,f(x)=3x+1≥0,
则f(f(x))=33x+1,
则由f(f(x))<4f(x)+1得33x+1<4(3x+1)+1,
设t=3x+1,则不等式等价为3t<4t+1,
设g(t)=3t-4t-1,则g(0)=0,g(2)=9-8-1=0,
即g(t)<0的解为0<t<2,即0<3x+1<2,
即-1<3x<1,得-$\frac{1}{3}$<x<$\frac{1}{3}$,
此时-$\frac{1}{3}$<x<0,
综上所述,-$\frac{1}{3}$<x<log32.
即不等式的解集为(-$\frac{1}{3}$,log32),
故选:D
点评 本题主要考查不等式的求解,利用分类讨论的数学思想将不等式进行转化为分段函数性质,利用换元法进行转化是解决本题的关键.综合性较强,难度较大.

练习册系列答案
相关题目
1.执行如图所示的程序,则输出的i的值为( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
11.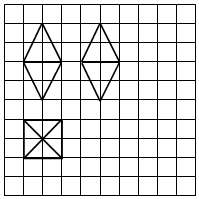 如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
 如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )| A. | 16 | B. | 8$\sqrt{5}$ | C. | 32 | D. | 16$\sqrt{5}$ |