题目内容
3.若函数f(x)=x3+2x2+x+a的零点成等差数列,则a=$\frac{2}{27}$.分析 利用导数研究函数的单调性与极值,由于函数f(x)=x3+2x2+x+a的零点成等差数列,可得极大值与极小值满足的条件.
解答 解:f′(x)=3x2+4x+1=0,
令f′(x)=0,解得x=-1或-$\frac{1}{3}$.
可知:-1或-$\frac{1}{3}$分别是函数f(x)的极大值点与极小值点.
∵函数f(x)=x3+2x2+x+a的零点成等差数列,
∴$f(-\frac{1}{3})+f(-1)$=0,
∴$(-\frac{1}{3})^{3}$+2×$(-\frac{1}{3})^{2}$-$\frac{1}{3}$+a+(-1)3+2×(-1)2-1+a=0,
解得a=$\frac{2}{27}$.
故答案为:$\frac{2}{27}$.
点评 本题考查了等差数列的性质、利用导数研究函数的极值、函数的零点,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.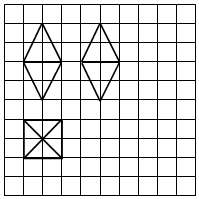 如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
 如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )| A. | 16 | B. | 8$\sqrt{5}$ | C. | 32 | D. | 16$\sqrt{5}$ |
12.曲线y=e${\;}^{\frac{1}{3}x}$在点(6,e2)处的切线与坐标轴所围成的三角形的面积为( )
| A. | $\frac{3}{2}{e}^{2}$ | B. | 3e2 | C. | 6e2 | D. | 9e2 |
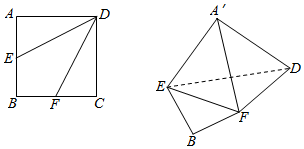 如图,边长为2的正方形ABCD中.
如图,边长为2的正方形ABCD中.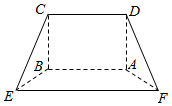 如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且AB∥EF,AF=2,EF=2AB=4AD=4$\sqrt{2}$,平面ABCD⊥平面ABEF.
如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且AB∥EF,AF=2,EF=2AB=4AD=4$\sqrt{2}$,平面ABCD⊥平面ABEF.