题目内容
定义方程f(x)=f′(x)的实数根x0叫做函数f(x)的“新不动点”,则下列函数有且只有一个“新不动点”的是 (写出所有正确的序号)
①g(x)=
x2
②g(x)=-ex-2x
③g(x)=lnx
④g(x)=sinx+2cosx.
①g(x)=
| 1 |
| 2 |
②g(x)=-ex-2x
③g(x)=lnx
④g(x)=sinx+2cosx.
考点:导数的运算
专题:导数的概念及应用
分析:分别求出每个函数的导数,然后解方程f(x)=f′(x),根据方程根的个数即可得到结论.
解答:
解:由题意方程f(x)=f'(x)的实数根x0叫做函数f(x)的“新不动点”,
①若g(x)=
x2 则g'(x)=x,由
x2=x,解得x=0或x=2.即有两个“新不动点”.
②若g(x)=-ex-2x,则g′(x)=-ex-2,由-ex-2x=-ex-2得2x=2,∴x=1,只有一个“新不动点”,满足条件.
③若g(x)=lnx,则g'(x)=
,由lnx=
,令r(x)=lnx-
,则r(x)在x>0上单调递增,可知r(1)<0,r(2)>0,只有一个“新不动点”,满足条件.
④若g(x)=sinx+2cosx.则g'(x)=cosx-2sinx,由sinx+2cosx=cosx-2sinx.得3sinx=cosx,即tanx=
,∴有无数多个“新不动点”.
综上只有②③满足条件.
故答案为:②③
①若g(x)=
| 1 |
| 2 |
| 1 |
| 2 |
②若g(x)=-ex-2x,则g′(x)=-ex-2,由-ex-2x=-ex-2得2x=2,∴x=1,只有一个“新不动点”,满足条件.
③若g(x)=lnx,则g'(x)=
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
④若g(x)=sinx+2cosx.则g'(x)=cosx-2sinx,由sinx+2cosx=cosx-2sinx.得3sinx=cosx,即tanx=
| 1 |
| 3 |
综上只有②③满足条件.
故答案为:②③
点评:本题主要考查导数的计算,是一个新定义的题,考查了推理判断的能力,理解定义,分别建立方程即可判断方程根的个数.

练习册系列答案
相关题目
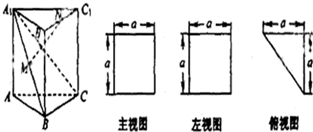 一个多面体的直观图和三视图(主观图、左视图、俯视图)如图所示,M、N分别为A1B、B1C1的中点.
一个多面体的直观图和三视图(主观图、左视图、俯视图)如图所示,M、N分别为A1B、B1C1的中点.