题目内容
17.解下列不等式:(1)|2x-1|<x;
(2)|2x-3|+|x-1|≥5.
分析 (1)(2)通过讨论x的范围解出各个区间上的x的范围,取并集即可.
解答 解:(1)x≥$\frac{1}{2}$时,2x-1<x,解得:x<1,
x<$\frac{1}{2}$时,1-2x<x,解得:x>$\frac{1}{3}$,
∴不等式的解集是:{x|$\frac{1}{3}<x<1$}; …(4分)
(2)原不等式可化为:
$\left\{\begin{array}{l}{x≥\frac{3}{2}}\\{2x-3+x-1≥5}\end{array}\right.$或$\left\{\begin{array}{l}{1<x<\frac{3}{2}}\\{3-2x+x-1≥5}\end{array}\right.$或$\left\{\begin{array}{l}{x≤1}\\{3-2x+1-x≥5}\end{array}\right.$
解得:$x≤-\frac{1}{3}$或x≥3.
点评 本题考查了绝对值不等式的解法,考查分类讨论思想,是一道基础题.

练习册系列答案
相关题目
5.已知某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 48 | B. | 4 | C. | 12 | D. | 16 |
12.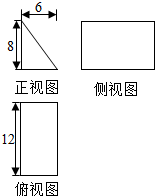 一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的表面积等于( )
一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的表面积等于( )
 一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的表面积等于( )
一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的表面积等于( )| A. | $\frac{32π}{3}$ | B. | 16π | C. | 32π | D. | $\frac{16π}{3}$ |
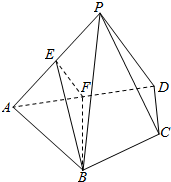 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD=4AP,∠BAD=∠PAD=60°,E,F分别是AP,AD的中点.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD=4AP,∠BAD=∠PAD=60°,E,F分别是AP,AD的中点.
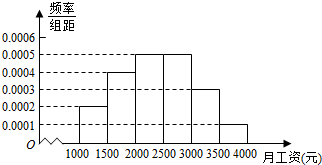 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图如图所示.(每个分组包括左端点,不包括右端点,如第一组表示[1000,1500).
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图如图所示.(每个分组包括左端点,不包括右端点,如第一组表示[1000,1500).