题目内容
6．试说明y=sin2x与y=sin2x的图象之间有什么样的关系．分析 由条件利用二倍角的余弦公式，函数y=Asin（ωx+φ）的图象变换规律，得出结论．
解答 解：∵y=sin2x，y=sin2x=$\frac{1-cos2x}{2}$，
∴把y=sin2x 的图象向右平移$\frac{π}{4}$个单位，可得y=sin2（x-$\frac{π}{4}$）=-cos2x的图象；
再把所得图象上的点的纵坐标变为原来的一半，可得y=-$\frac{1}{2}$cos2x的图象；
再把所得图象向上平移$\frac{1}{2}$个单位，可得y=sin2x=$\frac{1-cos2x}{2}$ 的图象．
点评 本题主要考查二倍角的余弦公式的应用，函数y=Asin（ωx+φ）的图象变换规律，属于基础题．
练习册系列答案
相关题目
17．已知点M是圆C：（x-1）2+（y-4）2=1上的点，不等式组$\left\{\begin{array}{l}{x+2y+4≥0}\\{x+4y≤0}\\{x+（a-1）y+2（a-1）≤0}\\{\;}\end{array}\right.$（a≠1）表示的平面区域为Ω，点P是Ω上一点，若|PM|的最小值为$\sqrt{17}$-1，则实数a的取值范围为（ ）
| A． | （-∞，1） | B． | （-3，1） | C． | （1，+∞） | D． | （1，3） |
14．设点A（2，0），B（4，2），则直线AB的斜率为（ ）
| A． | 1 | B． | -1 | C． | -2 | D． | 不存在 |
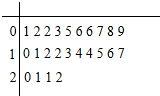为调查了解某药物使用后病人的康复时间，从1000个使用该药的病人的康复时间中抽取了24个样本，数据如下图中的茎叶图（单位：周）．专家指出康复时间在7周之内（含7周）是快效时间．
7．
如图，在圆x2+y2=4上任取一点P，过点P作x轴的垂线段PD，D为垂足．当点P在圆上运动时，线段PD的中点M的轨迹是椭圆，那么这个椭圆的离心率是（ ）
如图，在圆x2+y2=4上任取一点P，过点P作x轴的垂线段PD，D为垂足．当点P在圆上运动时，线段PD的中点M的轨迹是椭圆，那么这个椭圆的离心率是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |