题目内容
已知函数f(x)=x2+
-a(x+
)+a+2(x>0),若f(x)的值域为[-1,+∞],求a的值.
| 1 |
| x2 |
| 1 |
| x |
考点:利用导数求闭区间上函数的最值
专题:函数的性质及应用
分析:利用换元法,设x+
=t,则f(t)=f(t)=t2-at+a=(t-
)2+a-
,t≥2,根据函数的值域得到f(t)有最小值-1,分类讨论求出a的值.
| 1 |
| x |
| a |
| 2 |
| a2 |
| 4 |
解答:
解:∵f(x)=x2+
-a(x+
)+a+2=(x+
)2-a(x+
)+a,
设x+
=t,t≥2
=2,当且仅当x=1时取等号,
∴f(t)=t2-at+a=(t-
)2+a-
,t≥2
∵f(x)的值域为[-1,+∞),
当
≥2时,即a≥4时,函数f(t)min=f(
)=a-
=-1,
解得a=2+2
,或a=2-2
(舍去),
当
<2时,即a<4时,函数f(t)min=f(2)=4-2a+a=-1,
解得a=5,不符合题意,
综上所述a的值为2+2
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
设x+
| 1 |
| x |
x•
|
∴f(t)=t2-at+a=(t-
| a |
| 2 |
| a2 |
| 4 |
∵f(x)的值域为[-1,+∞),
当
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
解得a=2+2
| 2 |
| 2 |
当
| a |
| 2 |
解得a=5,不符合题意,
综上所述a的值为2+2
| 2 |
点评:本题主要考查了通过函数的值域参数的值的,采用了分类讨论的思想和转化的思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若方程x3+ax2+bx+c=0有三个不等实根x1,x2,x3则x1+x2+x3等于( )
| A、-a | B、-b | C、c | D、b |
斜率为1的直线l经过抛物线y2=2x的焦点,且与抛物线相交于A、B两点,则线段AB的长是( )
A、2
| ||
| B、2 | ||
C、4
| ||
| D、4 |
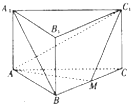 如图,已知三棱柱P-A1B1C1中,侧棱与底面垂直,AB=BC=2AA1,∠ABC=90°,M是BC的中点.
如图,已知三棱柱P-A1B1C1中,侧棱与底面垂直,AB=BC=2AA1,∠ABC=90°,M是BC的中点.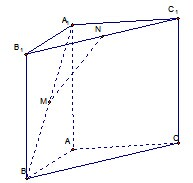 如图,直三棱柱ABC-A1B1C1,∠BAC=90°,AB=AC=
如图,直三棱柱ABC-A1B1C1,∠BAC=90°,AB=AC=
