题目内容
15.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的离心率为$\sqrt{2}$,过左焦点F1(-c,0)作圆x2+y2=a2的切线,切点为E,延长F1E交抛物线y2=4cx于点P,则线段PE的长为( )| A. | 2a | B. | 3a | C. | $({1+\sqrt{5}})a$ | D. | 4a |
分析 先有双曲线的性质和离心率得到c=$\sqrt{2}$a,再根据直线和圆相切,求出直线方程和抛物线方程联立方程,求出点P的坐标,即可求出PE的长
解答 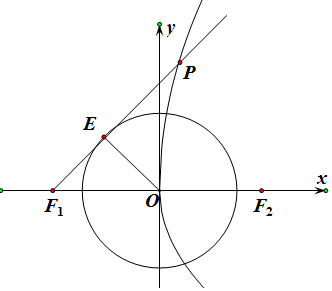 解:双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的离心率为$\sqrt{2}$,且e2=1+$\frac{{b}^{2}}{{a}^{2}}$,
解:双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的离心率为$\sqrt{2}$,且e2=1+$\frac{{b}^{2}}{{a}^{2}}$,
∴a=b,c=$\sqrt{2}$a,
∴圆的半径为OE=a,|OF1|=$\sqrt{2}$a,
∴∠EF1O=45°
∴直线PE的斜率为1,
∴直线PE的方程为y=x+$\sqrt{2}$a,
由$\left\{\begin{array}{l}{{y}^{2}=4\sqrt{2}ax}\\{y=x+\sqrt{2}a}\end{array}\right.$,
解得x=$\sqrt{2}$a,y=2$\sqrt{2}$a,
∴|PF1|=$\sqrt{(\sqrt{2}a+\sqrt{2}a)^{2}+(2\sqrt{2}a)^{2}}$=4a,
∴|PE|=|PF1|-|EF1|=4a-a=3a
故答案为:3a
点评 本题考查双曲线的性质,抛物线的性质、圆的性质、直线圆的位置关系,属于中档题.

练习册系列答案
相关题目
10.在△ABC中,A:B:C=4:1:1,则a:b:c=( )
| A. | 4:1:1 | B. | 2:1:1 | C. | 3:1:1 | D. | $\sqrt{3}$:1:1 |
20.已知函数f(x)=[x]的函数值表示不超过x的最大整数,例如,[-3.5]=-4,[2.1]=2,且集合A={x∈N*|2x≤x2},B={y|y=f(x),x∈[-1,1)},则可建立从集合A到集合B的映射个数为( )
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
7.已知A(2,4)关于直线x-y+1=0对称的点为B,则B满足的直线方程为( )
| A. | x+y=0 | B. | x-y+2=0 | C. | x+y-5=0 | D. | x-y=0 |
4.设数列{an},{bn}都是等差数列,且a1=12,b1=48,a2+b2=60,则由an+bn所组成的数列的第99项的值为( )
| A. | .60 | B. | 70 | C. | 99 | D. | 100 |
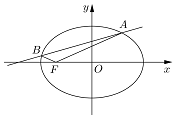 已知椭圆C以原点为中心,左焦点F的坐标是(-1,0),长轴长是短轴长的$\sqrt{2}$倍,直线l与椭圆C交于点A与B,且A、B都在x轴上方,满足∠OFA+∠OFB=180°;
已知椭圆C以原点为中心,左焦点F的坐标是(-1,0),长轴长是短轴长的$\sqrt{2}$倍,直线l与椭圆C交于点A与B,且A、B都在x轴上方,满足∠OFA+∠OFB=180°;