等差数列{an}的前10项和为30.前20项和为100.则它的前30项和是( )A．130B．170C．210D．260 题目和参考答案——青夏教育精英家教网—

题目内容

20．等差数列{a_n}的前10项和为30，前20项和为100，则它的前30项和是（　　）

A．

130

B．

170

C．

210

D．

260

分析由等差数列{a_n}的前n项和的性质：S_n，S_2n-S_n，S_3n-S_2n成等差数列．即可得出．

解答解：由等差数列{a_n}的前n项和的性质：S_n，S_2n-S_n，S_3n-S_2n成等差数列．
∴30+S₃₀-100=2×（100-30），
解得：S₃₀=210．
故选：C．

点评本题考查了等差数列的通项公式求和公式及其性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案

初中毕业学业考试模拟试卷湖南教育出版社系列答案

畅行课堂系列答案

学习周报系列答案

智能训练练测考系列答案

相关题目

10．在△ABC中，A：B：C=4：1：1，则a：b：c=（　　）

x	2	3	4	5	6
y	3	4	6	8	9

对于表中数据则根据最小二乘法的思想得拟合程度最好的直线是（　　）

y=$\frac{8}{5}$x-$\frac{2}{5}$

D．

y=$\frac{3}{2}$x

8．已知函数f（x）=e^x（x∈R）．
（1）证明：曲线y=f（x）与曲线$y=\frac{1}{2}{x^2}+x+1$有唯一公共点；
（2）设a＜b，比较$f（\frac{a+b}{2}）$与$\frac{f（b）-f（a）}{b-a}$的大小，并说明理由．

15．已知函数$f（x）=\frac{ax+b}{{{x^2}+1}}$是定义在（-1，1）上是奇函数，且$f（\frac{1}{2}）=\frac{2}{5}$．
（1）求函数f（x）的解析式；
（2）判断函数f（x）的单调性，并用定义证明．

5．A=$\left\{{（x，y）\left|{y≤\left.{\sqrt{4-{x^2}}，y≥0}\right\}}\right.}$，B={（x，y）|x+y≥2}，则A∩B所对应区域面积为（　　）

12．已知函数f（x）=$\frac{{e}^{x}}{ax}$（a＞0）
（1）求函数f（x）的图象在x=2处的切线方程；
（2）当a=1时，求f（x）在[t，t+1]（t＞0）上的最值．

9．

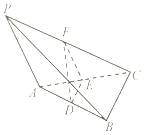已知，如图，P是平面ABC外一点，PA不垂直于平面ABC，E，F分别是线段AC，PC的中点，D是线段AB上一点，AB=AC，PB=PC，DE⊥EF．
（1）求证：PA⊥BC；
（2）求证：BC∥平面DEF．

10．已知曲线x²+y=8与x轴交于A，B两点，动点P与A，B连线的斜率之积为$-\frac{1}{2}$．
（1）求动点P的轨迹C的方程．
（2）MN是动点P轨迹C的一条弦，且直线OM，ON的斜率之积为$-\frac{1}{2}$．求$\overrightarrow{OM}•\overrightarrow{ON}$的最小值．

试题分类