题目内容
若函数f(x)=1oga(x+
-1)(a>0且a≠1)的定义域为(0,+∞),则实数a的取值范围是 .
| a |
| x |
考点:对数函数的图像与性质
专题:计算题,函数的性质及应用
分析:函数f(x)=1oga(x+
-1)(a>0且a≠1)的定义域为(0,+∞)可化为x+
-1>0在(0,+∞)上恒成立;从而得到2
>1;从而解得.
| a |
| x |
| a |
| x |
| a |
解答:
解:由题意,x+
-1>0在(0,+∞)上恒成立,
而x+
≥2
;
(当且仅当x=
,即x=
时,等号成立)
故2
>1;
故a>
,a≠1;
故答案为:a>
,a≠1.
| a |
| x |
而x+
| a |
| x |
| a |
(当且仅当x=
| a |
| x |
| a |
故2
| a |
故a>
| 1 |
| 4 |
故答案为:a>
| 1 |
| 4 |
点评:本题考查了基本不等式的应用及恒成立问题,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
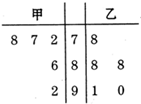 甲、乙两位同学在高二5次月考的数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是
甲、乙两位同学在高二5次月考的数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若方程ln(x+1)+2x-1=0的根为x=m,则( )
| A、0<m<1 |
| B、1<m<2 |
| C、2<m<3 |
| D、3<m<4 |