题目内容

在等比数列{an}中，a1+a3=10，a4+a6=
5
4
，求an和S4．
考点：等比数列的前n项和
专题：等差数列与等比数列
分析：设等比数列{an}的公比为q，由已知可解得a1和q，可得所求．
解答： 解：设等比数列{an}的公比为q，
∴a1+a3=a1（1+q2）=10，
a4+a6=a1（q3+q5）=
5
4
，
联立解得a1=8，q=
1
2
，
∴an=a1qn-1=8×(
1
2
)n-1=(
1
2
)n+2
∴S4=
a1(1-q4)
1-q
=15
点评：本题考查等比数列的通项公式和求和公式，属基础题．
练习册系列答案
相关题目
实数x，y满足条件
x+y-4≤0
x-2y+2≥0
x≥0
y≥0
，则22x-y的最小值为（　　）
A、
1
4
B、
1
2
C、1
D、4
已知向量
a
=（sin2x，-
1
2
），
b
=（
3
2
，cos2x），x∈R，设函数f（x）=
a
•
b
．
（Ⅰ）求f（x）的最小正周期．
（Ⅱ）求f（x）在[0，
π
2
]上的最大值和最小值．
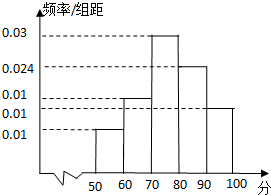某校为了解高一期末数学考试的情况，从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析，得到数学成绩频率分布直方图（如图所示），其中成绩在[50，60）的学生人数为6．
（Ⅰ）估计所抽取的数学成绩的众数；
（Ⅱ）用分层抽样的方法在成绩为[80，90）和[90，100]这两组中共抽取5个学生，并从这5个学生中任取2人进行点评，求分数在[90，100]恰有1人的概率．
某种产品的广告费支出x与销售额y（单位：万元）之间有如下对应数据：
x 2 4 5 6 8
y 30 40 60 50 70
若广告费支出x与销售额y回归直线方程为y=6.5x+a（a∈R）．
（I）试预测当广告费支出为12万元时，销售额是多少？
（Ⅱ）在已有的五组数据中任意抽取两组，求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率．
已知数列{an}的前n项和为Sn，若Sn=2an-1，则S2=
 
．
已知△ABC的周长为6，且sinA+sinB=2sinC，求边AB的长．
已知函数f（x）=alnx+（x-c）|x-c|，a＜0，c＞0．
（1）当a=-
3
4
，c=
1
4
时，求函数f（x）的单调区间；
（2）当c=
a
2
+1时，若f（x）≥
1
4
对x∈（c，+∞）恒成立，求实数a的取值范围；
（3）设函数f（x）的图象在点P（x1，f（x1））、Q（x2，f（x2））两处的切线分别为l1、l2．若x1=
-
a
2
，x2=c，且l1⊥l2，求实数c的最小值．
求函数y=
1
|sinx|
+
1
|cosx|
+
|cosx|
|sinx|
+
|sinx|
|cosx|
的最小值
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网