题目内容
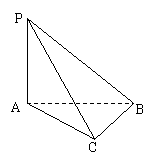
三棱锥P−ABC中,PA⊥平面ABC,AB⊥BC。
(1)证明:平面PAB⊥平面PBC;
(2)若PA=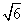 ,PC与侧面APB所成角的余弦值为
,PC与侧面APB所成角的余弦值为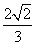 ,
,
PB与底面ABC成60°角,
求二面角B―PC―A的大小。
 |
(1)证明:∵PA^面ABC,\PA^BC, ∵AB^BC,且PA∩AB=A,\BC^面PAB
而BCÌ面PBC中,\面PAB^面PBC. ……5分
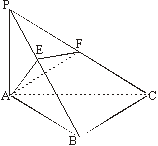 解:(2)过A作
解:(2)过A作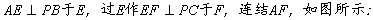
则ÐEFA为B−PC−A的二面角的平面角 ……8分
由PA=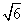 ,在RtDPBC中,
,在RtDPBC中, ÐCOB=
ÐCOB=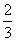
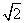 .
.
RtDPAB中,ÐPBA=60°. \AB=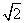 ,PB=2
,PB=2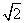 ,PC=3
,PC=3
\AE= 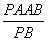 =
= 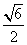
同理:AF=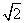 ………10分
………10分
\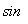 ÐEFA=
ÐEFA= 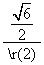 =
= 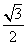 , \ÐEFA=60. ………12分
, \ÐEFA=60. ………12分
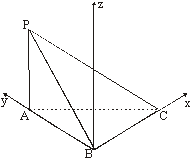
另解:向量法:由题可知:AB=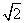 ,BC=1,建立如图所示的空间直角坐标系…………7分
,BC=1,建立如图所示的空间直角坐标系…………7分
B(0,0,0),C(1,0,0),A(0,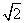 ,0),P(0,
,0),P(0,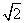 ,
,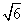 ),假设平面BPC的法向量为
),假设平面BPC的法向量为 =(x1,y1,z1),
=(x1,y1,z1),
 \
\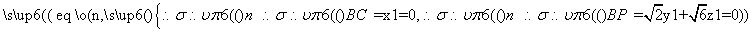
取z1=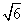 ,可得平面BPC的法向量为
,可得平面BPC的法向量为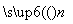 =(0,−3
=(0,−3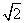 ,
,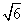 )………9分
)………9分
同理PCA的法向量为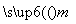 =(2,−
=(2,−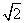 ,0)…………………11分
,0)…………………11分

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最大值为
的最大值为  ,则输出s属于( )
,则输出s属于( )
 B、
B、 C、
C、  D、
D、
 >
> ”,假设内容应是______________.
”,假设内容应是______________.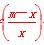 +f(m)<0,其中m∈R且m>0.
+f(m)<0,其中m∈R且m>0. )取得最大值时,x的值为
)取得最大值时,x的值为 ( )
( ) B
B .
. C.
C. D.
D.