题目内容
已知圆M:(x+1)2+y2=1,圆N:(x-1)2+y2=9,动圆P与圆M外切并且与圆N内切,圆心P的轨迹为曲线C.
(1)求C的方程;
(2)l是与圆P,圆M都相切的一条直线,l与曲线C交于A,B两点,当圆P的半径最长时,求|AB|.
解 (1)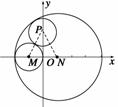 设圆P的半径为r,则|PM|=1+r,|PN|=3-r,∴|PM|+|PN|=4>|MN|,∴P的轨迹是以M,N为焦点的椭圆(左顶点除外),且2a=4,2c=2,∴a=2,c=1,∴b2=a2-c2=3.
设圆P的半径为r,则|PM|=1+r,|PN|=3-r,∴|PM|+|PN|=4>|MN|,∴P的轨迹是以M,N为焦点的椭圆(左顶点除外),且2a=4,2c=2,∴a=2,c=1,∴b2=a2-c2=3.
∴P的轨迹曲线C的方程为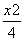 +
+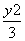 =1(x≠-2).
=1(x≠-2).
(2)由(1)知2r=(|PM|-|PN|)+2≤|MN|+2=4,
∴圆P的最大半径为r=2.此时P的坐标为(2,0).
圆P的方程为(x-2)2+y2=4.
①当l的倾斜角为90°,方程为x=0时,|AB|=2 ,
,
②当l的倾斜角不为90°,
设l的方程为y=kx+b(k∈R),
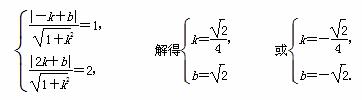 ∴l的方程为y=
∴l的方程为y=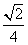 x+
x+ ,y=-
,y=-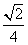 x-
x- .
.
联立方程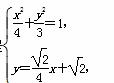 化简得7x2+8x-8=0,
化简得7x2+8x-8=0,
∴x1+x2=-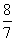 ,x1x2=-
,x1x2=-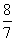 ,
,
∴|AB|=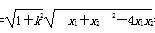 =
= .
.
当k=-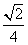 时,由图形的对称性可知|AB|=
时,由图形的对称性可知|AB|= .
.
综上,|AB|=2 或
或 .
.

练习册系列答案
相关题目
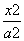 -
-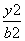 =1(a>0,b>0),双曲线的一个焦点到一条渐近线的距离为
=1(a>0,b>0),双曲线的一个焦点到一条渐近线的距离为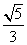 c(其中c为双曲线的半焦距长),则该双曲线的离心率为( ).
c(其中c为双曲线的半焦距长),则该双曲线的离心率为( ).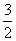 B.
B.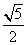 C.
C.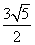 D.
D.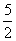
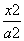 +
+ =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为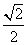 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.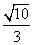 时,求k的值.
时,求k的值.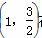 ,离心率e=
,离心率e=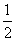 ,直线l的方程为x=4.
,直线l的方程为x=4.
 命题
命题 则( )
则( ) B.
B. 
 D.
D. 
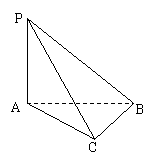
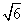 ,PC与侧面APB所成角的余弦值为
,PC与侧面APB所成角的余弦值为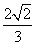 ,
,