题目内容
若a=2
cos50°(
-tan190°)sin(-
),则f(x)=loga
loga
(
≤x≤4)的值域为 .
| 2 |
| 3 |
| 21π |
| 4 |
| x |
| 4 |
| x |
| 2 |
| 1 |
| 4 |
考点:函数的值域
专题:函数的性质及应用,三角函数的求值
分析:先利用三角恒等变换将a的值求出来,然后再利用换元法将所求的函数化成二次函数求其值域.
解答:
解:因为2
cos50°(
-tan190°)
=2
cos50°(
-tan10°)
=2
cos50°(
)
=2
sin40°
=
=
=2
.
所以a=2
sin(-
)=2
sin(-6π+
)
=2
sin(
)=2
×
=2.
所以f(x)=(logax-loga4)(logax-loga2)
=(log2x)2-3log2x+2.
令t=log2x∈[-2,2].
则原函数化为y=t2-3t+2=(t-
)2-
.
该函数在[-2,
]上递减,在(
,2]上递增.
且t=-2时,y=12;t=2时,y=0;t=
时,y=-
.
故原函数的值域为[-
,12].
故答案为[-
,12].
| 2 |
| 3 |
=2
| 2 |
| 3 |
=2
| 2 |
| ||
| cos10° |
=2
| 2 |
| 2sin50° |
| sin80° |
=
2
| ||
| sin80° |
2
| ||
| sin80° |
| 2 |
所以a=2
| 2 |
| 21π |
| 4 |
| 2 |
| 3π |
| 4 |
=2
| 2 |
| 3π |
| 4 |
| 2 |
| ||
| 2 |
所以f(x)=(logax-loga4)(logax-loga2)
=(log2x)2-3log2x+2.
令t=log2x∈[-2,2].
则原函数化为y=t2-3t+2=(t-
| 3 |
| 2 |
| 1 |
| 4 |
该函数在[-2,
| 3 |
| 2 |
| 3 |
| 2 |
且t=-2时,y=12;t=2时,y=0;t=
| 3 |
| 2 |
| 1 |
| 4 |
故原函数的值域为[-
| 1 |
| 4 |
故答案为[-
| 1 |
| 4 |
点评:本题考查了三角恒等变换的化简求值问题以及二次函数在指定区间上的最值问题.注意换元法在本题中的应用.

练习册系列答案
相关题目
如表是函数u,v随自变量x变化的一组数据,由此判断u,v最符合的函数模型分别是( )
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| U | 0.0631 | 0.26 | 1.11 | 3.96 | 16.05 | 63.98 |
| v | 11.92 | 14.95 | 18.01 | 21.03 | 24.11 | 26.95 |
| A、二次函数型和一次函数型 |
| B、指数函数型和一次函数型 |
| C、二次函数型和对数函数型 |
| D、指数函数型和对数函数型 |
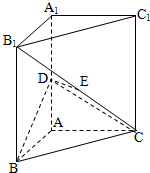 如图,直三棱柱ABC-A1B1C1,AB=AC=1,AA1=2.AB⊥AC.
如图,直三棱柱ABC-A1B1C1,AB=AC=1,AA1=2.AB⊥AC.