题目内容
已知函数f(x)=ln(x+1)-ax在x=1处的切线的斜率为l.
(1)求实数a的值及函数f(x)的最大值;
(2)证明:1+
+
+…+
>ln(n+1)(n∈N*).
(1)求实数a的值及函数f(x)的最大值;
(2)证明:1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)有函数f(x)=ln(x+1)-ax在x=1处的切线的斜率即是函数在x=1处的导函数值求得a,进而利用导数判断出函数的单调性求得最值;
(2)构造函数g(x)=ln(x+1)-x,求出g(x)的最大值为0,得出x≥ln(x+1),再令x=
(k∈N*),利用累加法得出结论.
(2)构造函数g(x)=ln(x+1)-x,求出g(x)的最大值为0,得出x≥ln(x+1),再令x=
| 1 |
| k |
解答:
解:(1)由已知可得函数的定义域为(-1,+∞)
∴a=-
…(2分)∴f(x)=ln(x+1)+
x∴f′(x)=
>0
∴f(x)在(-1,+∞)是单调递增∴f(x)的最大值不存在 …(6分)
(2)由(1)令g(x)=ln(x+1)-x,则g′(x)=-
,gmax(x)=g极大(x)=g(0)=0,
∴x≥ln(x+1),当且仅当x=0时等号成立
令x=
(k∈N*)
则x>0∴
>ln(1+
)=ln
=ln(1+k)-lnk
-------------------------------------------------------------------------…(12分)
|
∴a=-
| 1 |
| 2 |
| 1 |
| 2 |
| x+3 |
| 2(1+x) |
∴f(x)在(-1,+∞)是单调递增∴f(x)的最大值不存在 …(6分)
(2)由(1)令g(x)=ln(x+1)-x,则g′(x)=-
| x |
| 1+x |
∴x≥ln(x+1),当且仅当x=0时等号成立
令x=
| 1 |
| k |
则x>0∴
| 1 |
| k |
| 1 |
| k |
| 1+k |
| k |
|
-------------------------------------------------------------------------…(12分)
点评:考查学生会利用导数求曲线上过某点切线方程的斜率,会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值.掌握不等式恒成立时所取的条件.

练习册系列答案
相关题目
已知某锥体的三视图(单位:cm)如图所示,则该锥体的体积为( )
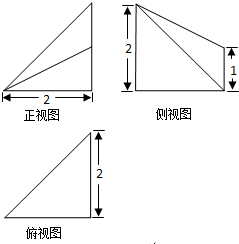

| A、2cm3 |
| B、4cm3 |
| C、6cm3 |
| D、8cm3 |
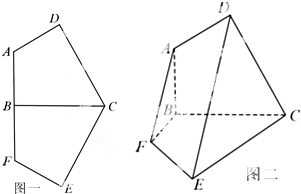 已知轴对称平面五边形ADCEF(如图1),BC为对称轴,AD⊥CD,AD=AB=1,CD=BC=
已知轴对称平面五边形ADCEF(如图1),BC为对称轴,AD⊥CD,AD=AB=1,CD=BC=