题目内容
求函数f(x)=lg(ax-k•2x)(a>0且a≠2)的定义域.
考点:对数函数的值域与最值
专题:计算题,函数的性质及应用
分析:由题意分k的正负以确定函数的定义域.
解答:
解:①当k≤0时,ax-k•2x>0恒成立;
故函数f(x)=lg(ax-k•2x)(a>0且a≠2)的定义域为R;
②当k>0时,
化简ax-k•2x>0得,
k<
=(
)x;
若0<a<2;解不等式可得,x<log
k;
故函数f(x)=lg(ax-k•2x)(a>0且a≠2)的定义域为(-∞,log
k);
若a>2;解不等式可得,x>log
k;
故函数f(x)=lg(ax-k•2x)(a>0且a≠2)的定义域为(log
k,+∞).
故函数f(x)=lg(ax-k•2x)(a>0且a≠2)的定义域为R;
②当k>0时,
化简ax-k•2x>0得,
k<
| ax |
| 2x |
| a |
| 2 |
若0<a<2;解不等式可得,x<log
| a |
| 2 |
故函数f(x)=lg(ax-k•2x)(a>0且a≠2)的定义域为(-∞,log
| a |
| 2 |
若a>2;解不等式可得,x>log
| a |
| 2 |
故函数f(x)=lg(ax-k•2x)(a>0且a≠2)的定义域为(log
| a |
| 2 |
点评:本题考查了函数的定义域的求法,同时考查了分类讨论的思想应用,属于基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
已知集合A={x|lgx≤1},B={x|2x≤1},则A∪B等于( )
| A、(0,10] |
| B、(-∞,0] |
| C、(0,+∞) |
| D、(-∞,10] |
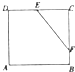 在如图所示的边长为6的正方形ABCD中,点E是DC的中点,且
在如图所示的边长为6的正方形ABCD中,点E是DC的中点,且| CF |
| 2 |
| 3 |
| CB |
| EF |
| AE |
| A、-18 | B、20 |
| C、12 | D、-15 |
已知函数f(2x-1)=3x-4,则f(3)等于( )
| A、-3 | B、-4 | C、1 | D、2 |
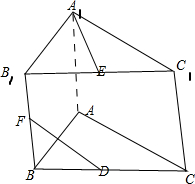 如图,在三棱柱ABC-A1B1C1中,AB=AC,侧棱AA1垂直于底面,D、E分别为BC、B1C1的中点,F为侧棱BB1上的一点.
如图,在三棱柱ABC-A1B1C1中,AB=AC,侧棱AA1垂直于底面,D、E分别为BC、B1C1的中点,F为侧棱BB1上的一点.