题目内容
6.i是虚数单位,复数$\frac{{2+{i^3}}}{1-i}$=( )| A. | $\frac{3+3i}{2}$ | B. | $\frac{1+3i}{2}$ | C. | $\frac{1+i}{2}$ | D. | $\frac{3+i}{2}$ |
分析 把分子利用虚数单位i的运算性质化简,然后分子分母同时乘以分母的共轭复数化简得答案.
解答 解:$\frac{2+{i}^{3}}{1-i}=\frac{2-i}{1-i}=\frac{(2-i)(1+i)}{(1-i)(1+i)}=\frac{3+i}{2}$,
故选:D.
点评 本题考查复数代数形式的乘除运算,是基础题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
4.已知角α的始边与x轴的正半轴重合,顶点在坐标原点,角α终边上的一点P到原点的距离为$\sqrt{2}$,若α=$\frac{π}{4}$,则点P的坐标为( )
| A. | (1,$\sqrt{2}$) | B. | ($\sqrt{2}$,1) | C. | ($\sqrt{2}$,$\sqrt{2}$) | D. | (1,1) |
17.在△ABC中,若AB=3,B=45°,BC=3$\sqrt{2}$,则△ABC的面积为( )
| A. | $2\sqrt{2}$ | B. | 4 | C. | $\frac{7}{2}$ | D. | $\frac{9}{2}$ |
11.已知全集U=R,集合A={-l,0,l,2},B={y|y=2x},图中阴影部分所表示的集合为( )


| A. | {-1,0} | B. | {l,2} | C. | {-l} | D. | {0,1,2} |
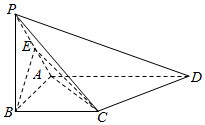 在四棱锥P-ABCD中,△ABC,△ACD都为等腰直角三角形,∠ABC=∠ACD=90°,E为PA的中点.
在四棱锥P-ABCD中,△ABC,△ACD都为等腰直角三角形,∠ABC=∠ACD=90°,E为PA的中点.