题目内容
13.已知函数f(x)=4x,若4,f(a1),f(a2),…,f(an),2n+3(n∈N*)构成等比数列.(I)求数列{an}的通项公式;
(Ⅱ)设 bn=$\left\{\begin{array}{l}\frac{1}{n},n为偶数\\ n+2,n为奇数\end{array}$求数列{$\frac{b_n}{a_n}}$}的前n项和为Sn.
分析 (I)运用等比数列的通项公式,结合函数的解析式,计算可得所求数列的通项公式;
(Ⅱ)设$\frac{b_n}{a_n}}$=cn,讨论n为偶数和奇数,运用分组求和和裂项相消求和,计算即可得到所求和.
解答 解:(I)由4,f(a1),f(a2),…,f(an),2n+3构成等比数列,
设公比为q,可得2n+3=4qn+1,解得q=2,
即有f(an)=${4}^{{a}_{n}}$=4•2n=2n+2,
可得an=$\frac{n+2}{2}$;
(Ⅱ)设$\frac{b_n}{a_n}}$=cn,由bn=$\left\{\begin{array}{l}\frac{1}{n},n为偶数\\ n+2,n为奇数\end{array}$,
当n为偶数时,cn=$\frac{2}{n(n+2)}$=$\frac{1}{n}$-$\frac{1}{n+2}$;当n为奇数时,cn=2.
当n为偶数时,Sn=(c1+c3+c5+…+cn-1)+(c2+c4+c6+…+cn)
=(2+2+2+…+2)+($\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{6}$+…+$\frac{1}{n}$-$\frac{1}{n+2}$)
=2•$\frac{n}{2}$+$\frac{1}{2}$-$\frac{1}{n+2}$=n+$\frac{1}{2}$-$\frac{1}{n+2}$;
当n为奇数时,Sn=Sn+1-Cn+1=n+1+$\frac{1}{2}$-$\frac{1}{n+3}$-($\frac{1}{n+1}$-$\frac{1}{n+3}$)
=n+$\frac{3}{2}$-$\frac{1}{n+1}$.
综上可得,$\left\{\begin{array}{l}{n+\frac{1}{2}-\frac{1}{n+2},n为偶数}\\{n+\frac{3}{2}-\frac{1}{n+1},n为奇数}\end{array}\right.$.
点评 本题考查等比数列的通项公式的运用,考查数列的求和方法:分组求和和裂项相消求和,运用分类讨论的思想方法是解题的关键,属于中档题.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案| A. | (-5,-3)∪(3,5) | B. | [-5,-3)∪(3,5] | C. | (-5,-3) | D. | (3,5) |
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
| A. | 3+4i | B. | 3-4i | C. | 5-4i | D. | 5+4i |
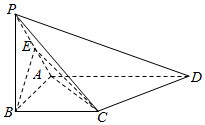 在四棱锥P-ABCD中,△ABC,△ACD都为等腰直角三角形,∠ABC=∠ACD=90°,E为PA的中点.
在四棱锥P-ABCD中,△ABC,△ACD都为等腰直角三角形,∠ABC=∠ACD=90°,E为PA的中点. 如图,在四棱锥P-ABCD中,底面ABCD为梯形,AB∥DC,平面PAD⊥平面ABCD,已知BD=2AD=4,AB=2DC=2$\sqrt{5}$,点M在PC上,PM=mMC.
如图,在四棱锥P-ABCD中,底面ABCD为梯形,AB∥DC,平面PAD⊥平面ABCD,已知BD=2AD=4,AB=2DC=2$\sqrt{5}$,点M在PC上,PM=mMC.