题目内容
在抛物线y2=2x上求一点P,使其到直线l:x+y+4=0的最距离最小,并求最小值.
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设P(x,y)为该抛物线上任一点,利用点到直线间的距离公式可求得点P到直线x+y+4=0的距离d的关系式,并求得dmin.
解答:
解:设P(x,y)为该抛物线上任一点,那么y2=2x,
则点P到直线的距离d=
=
[(y+1)2+7]≥
,当且仅当y=-1时,取“=”.
此时点P(
,-1).
即抛物线上的点P的坐标为P(
,-1)时,点P到直线x+y+4=0的距离最短,最小值为
.
则点P到直线的距离d=
| |x+y+4| | ||
|
| ||
| 4 |
7
| ||
| 4 |
此时点P(
| 1 |
| 2 |
即抛物线上的点P的坐标为P(
| 1 |
| 2 |
7
| ||
| 4 |
点评:本题考查抛物线的简单性质,考查点到直线间的距离公式与两点间的距离公式,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
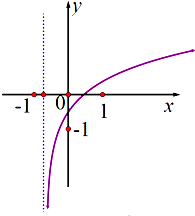
已知函数y=loga(x+b)(a>0且a≠1)的图象如图,则( )

| A、0<a-1<b<1<a |
| B、0<b<a<1<a-1 |
| C、0<a<b<1<a-1 |
| D、0<a<1<a-1<b |
函数f(x)=ln|x|-
x2的图象大致是( )
| 1 |
| 2 |
A、 |
B、 |
C、 |
D、 |
将函数y=cosx的图象向左平移φ(0≤φ<2π)个单位后,得到函数y=sin(x-
)的图象,则φ等于 ( )
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|