题目内容
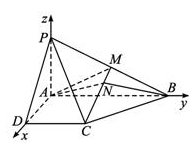
(本小题12分)如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB//DC, ,PA
,PA 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=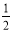 AB=1,M是PB的中点。
AB=1,M是PB的中点。

(1)证明:面PAD 面PCD;
面PCD;
(2)求AC与PB所成角的余弦值。
(1)见解析;(2)  .
.
【解析】
试题分析:方法一:∵PA⊥AD,PA⊥AB,AD⊥AB,以A为坐标原点,AD长为长度单位,
如图建立空间直角坐标系,则各点坐标为A(0,0,0)、B(0,2,0)、C(1,1,0)、D(1,0,0)、P(0,0,1)、M(0,1, 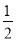 ).
).
(1)证明:∵ ∴
∴ ,
,
∴AP⊥DC.
又 由题设知AD⊥DC,且AP与AD是平面PAD内的两条相交直线,
∴DC⊥面PAD.
又∵DC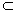 平面PCD,故面PAD⊥面PCD.
平面PCD,故面PAD⊥面PCD.
(2)【解析】
∵ ∴
∴
∴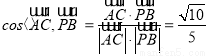 ,
,
故AC与PB所成的角的余弦值为 .
.
方法二:(1)证明:∵PA⊥面ABCD,∴PA⊥AB,∵∠DAB=90°,∴DA⊥AB,又PA∩DA=A,∴,

PA,DA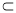 面PAD.∴AB⊥平面PAD.
面PAD.∴AB⊥平面PAD.
又AB∥CD
∴DC⊥平面PAD.
DC 面PCD,∴面PAD⊥面PCD.
面PCD,∴面PAD⊥面PCD.
(2)分别取BC,AB,PA中点为E,F,G,连结EF,FG,GE,AE,
∵BE=CE,BF=AF,∴EF∥AC,同理可得GF∥PB,
则∠PFE(或其补角)即为所求.
∵连结AE,可知AC=CB=BE=AE=2.
又 ,AB=2,,∴∠ACB=90°,又
,AB=2,,∴∠ACB=90°,又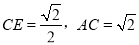 ,∴
,∴ ,
,
∵∠PAE=90°,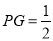 ,∴
,∴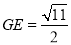 ,∵
,∵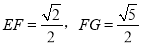
∴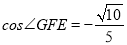 ,故AC与PB所成的角的余弦值为
,故AC与PB所成的角的余弦值为 .
.
考点:考查了面面垂直的判定,异面直线所成的角
点评:此题可以应用空间向量研究线线关系,证明线线垂直,求线线角;也可以利用面面垂直的判定定理证明,把异面直线所成的角转化为相交直线所成的角

练习册系列答案
相关题目
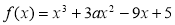 ,若
,若 在
在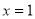 处有极值
处有极值 的值
的值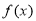 的极值
的极值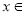
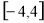 ,都有
,都有 ,求实数
,求实数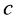 的取值范围
的取值范围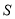 的值为( )
的值为( )
 被称为狄利克雷函数,其中
被称为狄利克雷函数,其中 为实数集,
为实数集,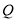 为有理数集,则关于函数
为有理数集,则关于函数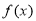 有如下四个结论:
有如下四个结论: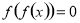 ; ②函数
; ②函数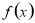 是偶函数; ③任取一个不为零的有理数
是偶函数; ③任取一个不为零的有理数 对任意的
对任意的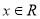 恒成立; ④存在三个点
恒成立; ④存在三个点 ,使得
,使得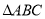 为等边三角形.
为等边三角形. ( )
( ) B.
B. C.
C. D.
D.
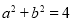 为真是
为真是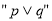 为真的充分不必要条件;
为真的充分不必要条件;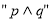 为假是
为假是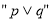 为真的充分不必要条件;
为真的充分不必要条件;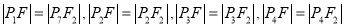 为假的必要不充分条件;
为假的必要不充分条件; 为真是
为真是 为假的必要不充分条件。正确的是____ ____。
为假的必要不充分条件。正确的是____ ____。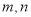 是两条不同直线,
是两条不同直线,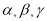 是三个不同平面,下列命题中正确的是( )
是三个不同平面,下列命题中正确的是( )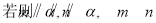
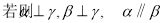
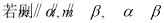
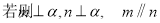
 = _________.
= _________.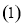 已知
已知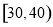 、
、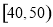 、
、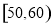 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求 ,
,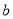 的值;
的值;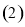 该电子商务平台将年龄在
该电子商务平台将年龄在 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购物者中抽取10人,并在这10人中随机抽取3人进行回访,求此三人获得代金券总和
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购物者中抽取10人,并在这10人中随机抽取3人进行回访,求此三人获得代金券总和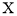 的分布列与数学期望.
的分布列与数学期望.