题目内容
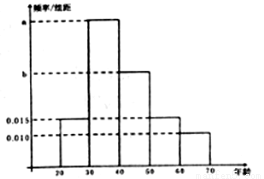
(本小题满分12分)根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如下图显示.
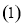 已知
已知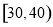 、
、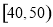 、
、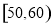 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求 ,
,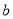 的值;
的值;
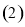 该电子商务平台将年龄在
该电子商务平台将年龄在 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购物者中抽取10人,并在这10人中随机抽取3人进行回访,求此三人获得代金券总和
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购物者中抽取10人,并在这10人中随机抽取3人进行回访,求此三人获得代金券总和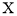 的分布列与数学期望.
的分布列与数学期望.
(1)  ,
, ;(2)
;(2)
| 150 | 200 | 250 | 300 |
|
|
|
|
|
 .
.
【解析】
试题分析:(1)根据频率直方图中结论:所有频率之和为1,则有: ,即有:
,即有: ,又由条件:
,又由条件: 、
、 、
、 三个年龄段的上网购物者人数成等差数列,则有:
三个年龄段的上网购物者人数成等差数列,则有: ,解方程组得:
,解方程组得: ,
, ;(2) 根据(1)中:
;(2) 根据(1)中: ,可得高消费人群所占比例为
,可得高消费人群所占比例为 ,利用分层抽样从样本中抽取10人,其中属于高消费人群的为6人,属于潜在消费人群的为4人.从中取出三人,并计算三人所获得代金券的总和
,利用分层抽样从样本中抽取10人,其中属于高消费人群的为6人,属于潜在消费人群的为4人.从中取出三人,并计算三人所获得代金券的总和 ,则
,则 的所有可能取值为:150,200,250,300. 运用概率公式求得:
的所有可能取值为:150,200,250,300. 运用概率公式求得: ,
, ,
, ,
, ,用列表的形式即可得到概率分布表,运用数学期望公式求得:
,用列表的形式即可得到概率分布表,运用数学期望公式求得: .
.
试题解析:(1)由图可知 ,
, . (4分)
. (4分)
(2) 利用分层抽样从样本中抽取10人,其中属于高消费人群的为6人,属于潜在消费人群的为4人. (6分)
从中取出三人,并计算三人所获得代金券的总和 ,
,
则 的所有可能取值为:150,200,250,300.
的所有可能取值为:150,200,250,300.
 ,
,  ,
,
 ,
,  ,
,
| 150 | 200 | 250 | 300 |
|
|
|
|
|
(10分)
且 . (12分)
. (12分)
考点:1.统计与概率的相关知识;2.离散型随机变量的分布列;3.数学期望







 ,PA
,PA 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=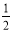 AB=1,M是PB的中点。
AB=1,M是PB的中点。
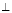 面PCD;
面PCD;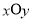 中,曲线
中,曲线 的参数方程为
的参数方程为 (
(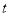 为参数),以原点
为参数),以原点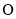 为极点,以
为极点,以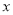 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线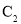 的极坐标方程为
的极坐标方程为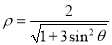 .
.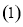 求曲线
求曲线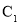 的普通方程与曲线
的普通方程与曲线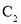 的直角坐标方程;
的直角坐标方程; 试判断曲线
试判断曲线 与
与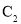 是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.
是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.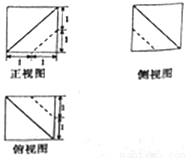
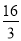 B.
B.
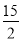 D.
D.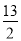
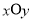 中,曲线
中,曲线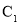 的参数方程为
的参数方程为 (
(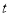 为参数),以原点
为参数),以原点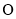 为极点,以
为极点,以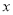 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线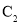 的极坐标方程为
的极坐标方程为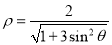 .
. 求曲线
求曲线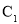 的普通方程与曲线
的普通方程与曲线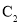 的直角坐标方程;
的直角坐标方程;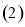 试判断曲线
试判断曲线 与
与 是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.
是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由. 的展开式中常数项为 .
的展开式中常数项为 .
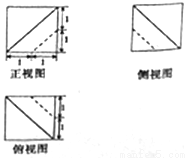
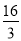 B.
B.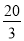
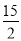 D.
D.
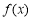 满足
满足 ,当
,当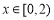 时,
时, 函数
函数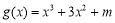 .若
.若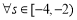 ,
,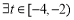 ,不等式
,不等式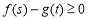 成立,则实数m的取值范围是( )
成立,则实数m的取值范围是( )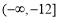 (B)
(B)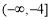
 (D)
(D)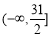
 分别为双曲线
分别为双曲线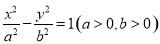 的左,右焦点,P为双曲线右支上的一点,且
的左,右焦点,P为双曲线右支上的一点,且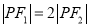 .若
.若 为等腰三角形,则该双曲线的离心率为_________.
为等腰三角形,则该双曲线的离心率为_________.